アナタの想像力をフルに働かせて応力計算:仕事にちゃんと役立つ材料力学(3)(2/2 ページ)
腰掛けた椅子だって、実は変形している。変形したということは、応力が発生している。目に見えない現象は、頭でしっかりイメージを作る。
話を僕流に戻しましょう。「恐竜や象の足は、太い」「アリやコオロギの足は、細い」。これは、重力に対応するために進化した一例です。一般的に自重があればあるほど、自分を支えるのに苦労します。特に振動問題を扱う場合には、「重さ」というパラメーターは非常に重要になってきます。
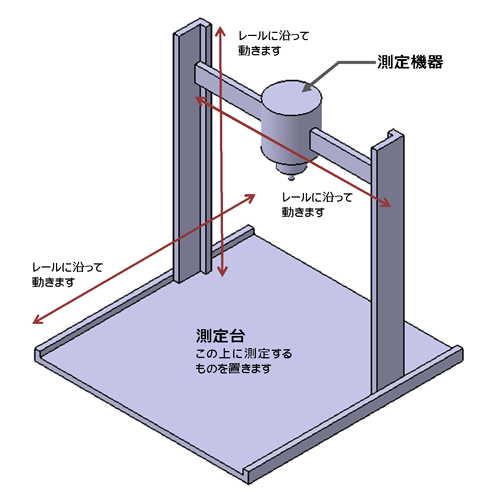
また構造的に「重さ」を配慮しなければならない場合もあります。僕がずぅ〜っと昔にやった小型3次元形状測定器の構造解析で、自重の大切さを思い知ったことがあります(図5)。
3次元形状測定器には、測定する物体を置く台があります。その両端に支柱があって、それが滑らかにレールで移動します。その支柱に橋が渡してあります。それも支柱に沿って滑らかに移動します。その橋を貫くように測定器があります。それがまた滑らかに橋を移動します。
測定器の下端で測定する物体に触れて、その3次元的な座標を読み取っていくものです。2次元の座標を読み取るものに「デジタイザ」という機械がありましたが、要はその3次元版というわけです。
いまだと、小型化技術が進んでいて、測定器は重さが感じられないほど小さくなるのでしょうね。ところが当時は、結構な重さがありました。測定器を手に取ったときのズッシリとした感覚をいまだに覚えています。
さて、そんな重さを持つ測定器でしたから、測定器を支える橋部材も支柱も十分な強度がなければなりません。太くすれば強度は稼げますが、動かすのが大変です。かといって、細くしてしまうと測定器が中央に来れば来るほど、橋部材がたわんで、測定に大きな誤差が出てしまいます。
これに似た構造は皆さんの周りでもよく見掛けると思います。ちょっとWebで検索してみたら、顕微鏡で以下のようなものが出てきました。
ね、これ重そうでしょう? しかも自重が焦点距離にモロに効いてきそうです。
特に重いモノを扱う場合は、自重に気を付けましょう、というお話でした。自重も荷重の1つであるということです。そして荷重があれば、応力が発生するということです。
応力を計算してみよう
ここまでの解説では、「内力=応力」と思われたかもしれません。それはそれで大きな意味では正しいのですが、もう少しだけ応力の定義に踏み込こんでみましょう。
「応力とは、荷重に対して着目物体に発生する内力(抵抗する力)のことで、単位面積当たりの力で表す」
これを式を使って書くと、以下のようになります。「数式は使わず」ということでしたけど、これくらいの式ならお許しいただけるでしょうか?
応力=荷重/断面積
応力は荷重を単位面積当たりの力に換算したものなのです。ここでの断面積とは、図2で登場した「仮想的に分断した面」の面積です。
さて、ここでカンタンな練習問題を1つやってみましょう。
*** 一部省略されたコンテンツがあります。PC版でご覧ください。 ***
“100kg”という重さをちゃんとイメージしてくださいね? 「自分何人分だぁ?」とか、「5キロの米袋の20個分かぁ?」とか。ちなみに大人のツキノワグマの体重が約100kgです。材料力学は、イメージすることが大切ですよ!
「そんな重いと、天井から棒が抜けちゃうよぉ」とか「棒がちぎれちゃう」なんてことは一切考えないで、さっきの式に数字を当てはめてみてください。とってもカンタンな計算に思えますが、実際、カンタンな計算なんですよ。この問題はいつも解析工房でやるのですが、たまーに間違える人がいます。
それでは、電卓でチョチョイと計算してみましょう。できれば、そのへんの紙に式を書きながら計算してみてください。
以下に解答があります。
さて、どうでしたか?
ちゃんと単位は書いてありますか? まず、単位を書いていないと、大幅減点です。いちいち単位を書くクセを付けておいてくださいね。
そして数字はどうでしたか? 単位に応じて、小数点の位置が変わります。電卓の窓に「1.274」と出た人もいれば、「12740000」と出た人もいれば、「0.0001274」と出た人もいるでしょう。ここで大抵の人は、「『1274』という数字があって、同じ順序で並んでいるんだから、正解だよね」と思ってしまうのです。それは単位を意識していない証拠です。どうか、単位を常に考える習慣を付けてくださいね。
そういうわけで答えは、「丸棒の断面の1mm2に、1.274kgfの応力が発生している」ということになります。1mm2 という面積をイメージしてみてください。われわれのサイズ感から考えると、相当、小さいですよね。そこになんと、1kgfを超える応力が発生しているのです。1kgfをイメージしてみてください。例えば、お肉はどうでしょう? 「ステーキの1キロ」って、どんだけデカいか……。
ここで、ちょっと考えてみましょう。
「ところで、この棒、ちぎれるの? ちぎれないの?」
もしこの丸棒が、プラスチックという「材料」だったら、ほぼ確実に、ちぎれてしまうでしょう。この丸棒が鉄という「材料」だったら、100kgの重さを見事に支えるでしょう。
つまり材料によって、ちぎれるかちぎれないかが決まるということです。
◇
練習問題が1つ終わったところで、今回はこれくらいにしておきましょう。次回は、応力の単位についてさらに理解を深め、応力の種類について解説します。 (次回に続く)
*** 一部省略されたコンテンツがあります。PC版でご覧ください。 ***
Copyright © ITmedia, Inc. All Rights Reserved.