実例で学ぶ公差設計 〜穴と軸から不良率を推測する〜：若手エンジニアのための機械設計入門（8）（2/3 ページ）

3D CADが使えるからといって、必ずしも正しい設計ができるとは限らない。正しく設計するには、アナログ的な知識が不可欠だ。連載「若手エンジニアのための機械設計入門」では、入門者が押さえておくべき基礎知識を解説する。第8回では、穴と軸のはめ合いを題材に、公差設計に確率統計を応用し、不良率をどのように予測できるかを取り上げる。

[土橋美博／スワニー，MONOist]

Cpの示す数値の意味は何か？

　Cpは、単に数式で求められる値にとどまらず、その大きさによって工程の安定性を判断することができます。では、具体的にどのような意味を持つのでしょうか。

• Cpが高い → 規格幅に対してバラつきが小さい → 安定した工程
• Cpが低い → 規格幅ギリギリ、あるいは狭い → 不安定な工程

　例えば、Cp＝1.33の場合、約±4σの範囲が規格内に収まります。このときの不良率はおよそ0.0063％と非常に低く、量産においても安心できる水準といえます。

一般的なCp値のイメージ

　このように、Cpの値は工程の安定性や不良率の大きさを判断する基準になります。では、現場ではCpの値をどのように目安として考えているのでしょうか。以下に代表的なイメージを示します。

• Cpが高い工程 → 安定しているので安心して量産できる
• Cpが1.0ギリギリ → 基準は満たすが、不良が出る可能性もある
• Cpが低い → ロットごとに品質がバラバラで、検査落ちが多い

　筆者は装置設備産業での経験が長いのですが、この工程能力指数（CpやCpk）は、製品品質の評価だけでなく、個々の設備性能を測る指標としても活用されています。

丸棒がパイプの穴に挿入できない確率を求める

　では、丸棒がパイプの穴に挿入できない確率を実際に求めてみましょう。

　パイプの内径と丸棒の外径は片側公差で与えられているため、まずは「中央値化」を行います。中央値化とは、片側公差を両側公差に変換して表現する方法です。

　ここで、パイプと丸棒はいずれもCp＝1で管理されていると仮定します。

　この条件から、それぞれの寸法は以下のように正規分布で表されます。

• パイプ：N（8.075，0.025²）
• 丸棒：N（7.925，0.025²）

　次に、パイプの内径と丸棒の外径の隙間を考えます。平均値の差を計算すると、8.075−7.925＝0.15となり、これを隙間の平均値μ＝0.15とします。では、この隙間の分布はどのようになるでしょうか。ここで重要になるのが「分散の加法性」です。

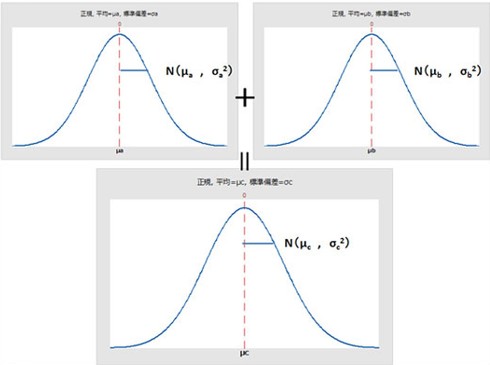
分散の加法性とは何か？

　分散とは、バラつきの大きさを数値で表したものです。値が大きければバラつきも大きく、値が小さければバラつきも小さいことを意味します。

　今回の例のように、パイプの穴径にもバラつきがあり、丸棒の外径にもバラつきがある場合、この2つを組み合わせたときの「隙間のバラつき」は、それぞれのバラつきが合わさって大きくなります。このときに成り立つのが分散の加法性であり、“分散はそのまま足し算できる”という性質を持っています。

　パイプのバラつきをσa²、丸棒のバラつきをσb²とすると、全体のバラつき（隙間の分散）σc²は、σc²＝σa²＋σb²のように計算されます。

図2　分散の加法性［クリックで拡大］

　分散の加法性を適用すると、隙間の分散は次のように求められます。

σ²＝0.025²＋0.025²＝0.00125

　従って、標準偏差は√0.00125≒0.035となります。

　これにより、隙間の分布は以下のように表されます。

N（0.15，0.035²）

　次に、隙間がゼロ（0）以下、つまり軸が穴に入らない場合の確率を求めます。

　標準正規分布表（図3）を用いると、その確率はε＝8.93×E^-6（約0.000893％）となります。従って、軸が穴に入らない確率は非常に低いと考えられます。

図3　標準正規分布表［クリックで拡大］