CAEによる流体解析の手順を確認／実行し、紙と鉛筆による結果と比べる：CAE解析とExcelを使いながら冷却系設計を自分でやってみる（10）（2/4 ページ）

CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる／できるようになる”ことを目指す連載。連載第10回では、CAEによる流体解析の手順を確認した後、実行結果と“紙と鉛筆”による結果とを比較する。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

手順4：流体解析ソフトでのセットアップ

　いよいよ、流体解析ソフトでのセットアップ作業に入ります。使用するCAE解析ソフトが異なっていても、流体解析に必要な情報は共通しています。それらの項目を表1にまとめました。No.1から順に説明していきます。

No.	アイテム	目的
1．	ドメインの定義	どの領域が流体であり、どの領域が固体であるかを教える
2．	流体モデルの定義	流体領域を層流として扱うか、乱流として扱うかを教える
3．	物性値の定義	流体および固体の物性値を教える
4．	境界条件の定義	どの面が入り口で、どの面が出口を教える
5．	壁面の定義	流体がパイプと接している面（壁面）の情報を教える
6．	対称面の定義	形状が対称の場合、モデルを簡略化（2分の1モデルなど）するために対称面を教える
7．	初期値の設定	流速、圧力、温度などの初期値を教える
8．	解法の定義	定常解析か過渡応答解析かを教える
表1　CAE解析ソフトに教える情報

　No.1の「ドメインの定義」では、どの領域が流体で、どの領域が固体であるかを教えます。これは流体解析において基本的な内容です。後ほど紹介するシミュレーションでは、流体ドメインのみを定義しています。

　No.2の「流体モデルの定義」では、自分でレイノルズ数を計算し、層流として解析するのか、乱流として解析するのかを教えます。CAE解析ソフトが自動的に判別してくれるわけではありません。層流の場合は選択肢が1つしかありませんが、乱流の場合は20個くらい選択肢があります。この点についてはいずれ説明します。

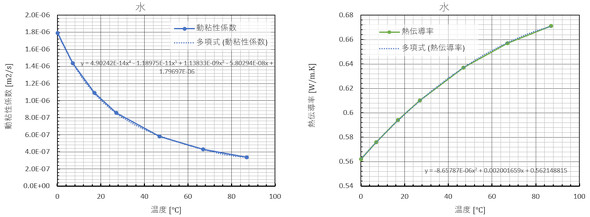
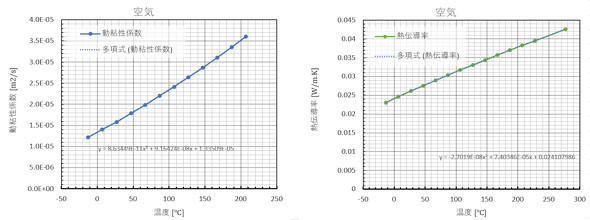
　No.3の「物性値の定義」では、流体および固体の物性値を教えるか、指定します。水や空気の物性値は温度によって敏感に変化するため、図6、図7のようにグラフにして多項式近似の式を作っておくと便利です。本シリーズの目的は「冷却系の設計計算Excelシートを作成すること」なので、シート内に多項式近似した物性値を求めるセルを作っておくことは必須です。

図6　水の動粘性係数と熱伝導率［クリックで拡大］

図7　空気の動粘性係数と熱伝導率［クリックで拡大］

　ここで、筆者の失敗談を1つ紹介します。水は温度が上がるとサラサラになって粘性係数が下がります。これと同じように、気体も粘性が下がるものと信じ込んで設計をしたことがあります。しかし、図7に示すように、気体は温度が上がると粘性も上昇します。

　次は、No.4の「境界条件の定義」です。通常、入り口では平均流速、温度を指定し、出口には圧力を指定します。このとき、ゲージ圧と絶対圧を取り違えないよう十分に注意してください。また、入り口では平均流速の代わりに圧力を指定することも可能です。

　No.5は「壁面の定義」です。壁面近傍では流速がゼロとなるため、そうなるようにシミュレーションします。この場合、「no slip wall」として指定します。以前、水とガスを接触させる接触槽（ちょっとしたプールのような構造）を解析したことがあります。プールの水面は自由表面となり、その上での流速はゼロではありませんね。そのため、「slip wall」を指定しました。ちなみに、波のように変形する自由表面を扱えるCAE解析ソフトを使う手もあります。ただし、自由表面の計算は非常に時間がかかるため、どうしても自由表面の形が知りたい場合に限って使用していました。

　そして、No.6の「対称面の定義」です。流体領域の形状が対称である場合は、積極的に2分の1モデルや4分の1モデルなどの簡略化したモデルに変更します。2分の1モデルや4分の1モデルの対称面には、その面が対称面であることをCAE解析ソフトに教えます。

　対称面があると、対称面垂直方向の速度はゼロになります。1分の1モデルでは、まれにうまく境界条件を設定できないことがありますが、対称面を使うとうまく表現できます。これは、弾性変形を扱う有限要素法ソフトでも同様です。

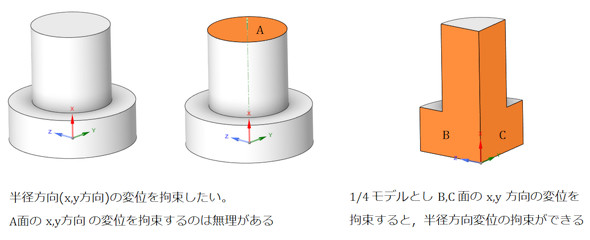
　補足として、応力解析の例を挙げて説明します。図8に、回転対称形の物体の応力解析において、半径方向変位を拘束したい場合を示します。A面の半径方向（x、y方向）変位を拘束すると、A面に変な応力が発生します。このようなときは4分の1モデルとして、B、C面の変位を拘束すると厳密な半径方向変位拘束を表現できます。対称形の解析では、単に節点数を削減するためだけでなく、変位拘束をうまく表現するためにも対称モデルを使います。

図8　回転対称形の応力解析での半径方向変位拘束［クリックで拡大］

　有限体積法は繰り返し計算で解を出しますが、No.7の「初期値の設定」をすると、解の収束が早まることがあります。CAE解析ソフトによる自動設定機能もあります。

　No.8の「解法の定義」では、流速や圧力が時間進行に対して変化しない問題（定常解析）であるか、時間的に変化する問題（過渡応答解析）であるかを指定します。過渡応答解析の場合、No.7の「初期値の設定」が必須となります。また、時間刻みΔtを指定する必要があります。Δtが大き過ぎると、計算精度が低下する可能性があることは想像しやすいと思います。

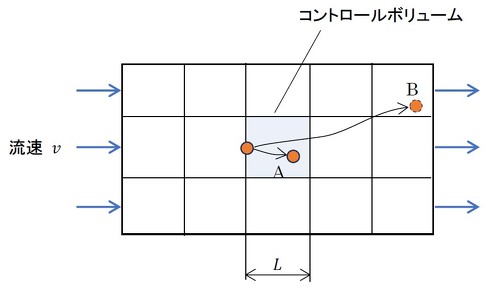
　図9に、時間刻みΔt間の流体粒子の移動を示します。説明を簡単にするため、コントロールボリュームは6面体としています。Δt後に流体粒子はAの位置にいてほしいですね。もし、Bまで移動していたとすると、Bまでの移動は一発計算の結果であって、移動の途中をうまく計算できていないことになります。

図9　時間刻みΔt間の流体粒子の移動［クリックで拡大］

　Δt後に流体粒子がAの位置に移動しているための条件は式1となります。

式1

　今、以下のような数Cを定義します（式2）。

式2

　式1の条件を満たすためには、C＜1である必要があります。このCは「クーラン数」と呼ばれ、時間刻みΔtを決める目安となります。