ボルト締結体に作用できる許容繰り返し荷重：CAEを正しく使い疲労強度計算と有機的につなげる（17）（2/4 ページ）

金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第17回では「ボルト締結体に作用できる許容繰り返し荷重」について取り上げる。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

ボルトに発生する応力振幅と許容繰り返し荷重：ボルト2本

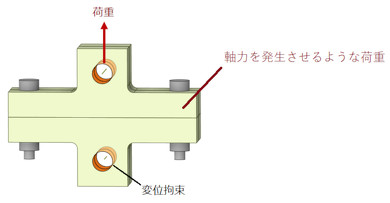
　ボルト2本の場合を説明します。ボルト1本では荷重の作用線とボルトの軸とが一致していますが、ボルト複数本では荷重の作用線がボルトの軸と一致しません。図4に荷重条件を示します。荷重を2段階に分けて、1回目の荷重条件でボルトの軸力を発生させ、2回目の荷重条件でボルトの締結状態を維持しつつ荷重を作用させます。

図4　境界条件［クリックで拡大］

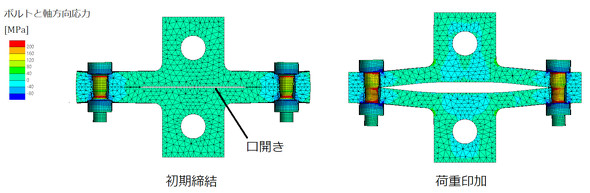
　図5に解析結果を示します。変位倍率を上げると分かるのですが、初期締結状態で口開きが発生しています。

図5　解析結果：ボルト2本［クリックで拡大］

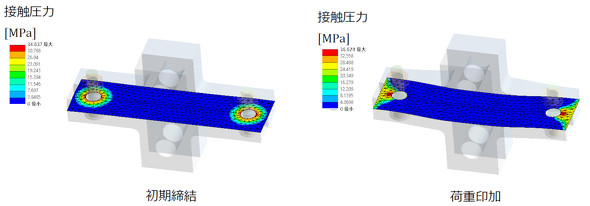
　図6に被締結体の接触圧力を示します。初期締結状態では青色領域（接触圧力がほぼゼロの領域）が大部分であることに注目します。つまり、締結面の全部が密着しているわけではありません。その結果、図5左図のように口開きが発生します。「初期締結状態で口開きが発生し、被締結体は全面にわたり密着していないこと」がボルト締結のスタンダートかもしれません。

図6　被締結体の接触圧力［クリックで拡大］

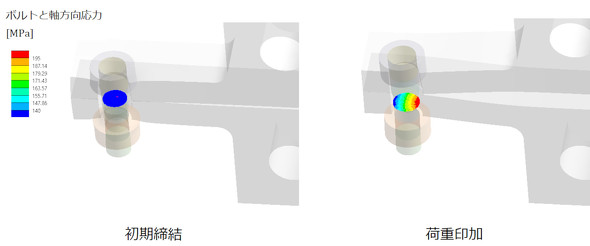
　図7にボルト断面の応力分布を示します。ボルト2本ではボルトに曲げ応力が発生して応力振幅がかなり大きくなることが分かります。

図7　ボルト断面の応力分布［クリックで拡大］

　ここでは口開きに対して目をつぶることにして、荷重時のボルトの応力振幅が疲労強度の半分になる荷重を求めたところ、7426［N］となりました。ボルト1本当たりはこの半分の3623［N］となります。では、ボルト1本のときと比較してみましょう。式2にΦ値が最も大きな0.130［-］を代入すると14841［N］です。被締結体に作用できる許容繰り返し荷重の比較を表2に示します。ボルト2本構成とすると「ドカーン」と許容繰り返し荷重が減少します。

	単位	ボルト1本	ボルト2本
内力係数Φ	−	0.13	有限要素法で求まる値
許容繰り返し荷重	N	14841	7426
許容繰り返し荷重 ボルト1本当たり	N	14841	3623
表2　被締結体に作用できる許容繰り返し荷重

　例えば、ボルトが4本あるときに、“ボルト1本のモデルの内力係数からボルト1本当たりが負担できる繰り返し荷重を求め、それを単純に4倍する”という設計がかなり危ないことをご理解いただけたでしょうか。

被締結体の許容繰り返し荷重：ボルト2本でのサーベイ

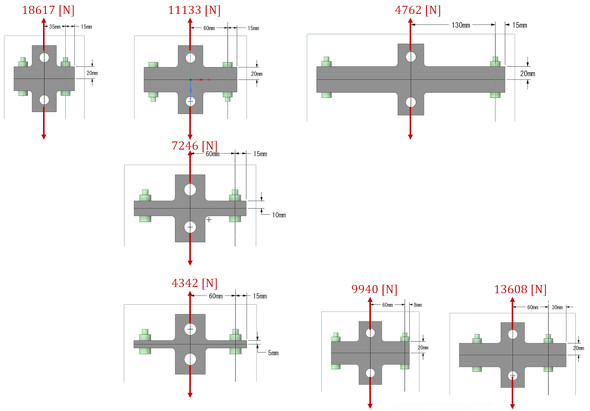
　図5の変形図を見ると、ボルトに発生する曲げ応力は被締結体の形状によって変化し、この結果被締結体の作用させる許容繰り返し荷重も被締結体の形状によって変化すると推測されます。形状を変えてサーベイを行いました。図8に被締結体の形状を変えたときの許容繰り返し荷重を示します。許容繰り返し荷重はボルトの発生する応力振幅がちょうど疲労強度の2分の1となる荷重です。2分の1というのは安全率を2［-］としたからです。

図8　被締結体に作用させる許容繰り返し荷重［クリックで拡大］

　「やっぱりこうなるのか」と思っていましたが、被締結体の形状を変えると許容荷重は大きく変化しました。同時に、多くのケースでΦ＝0.130［-］として求めた許容荷重よりも小さくなりました。内力係数を使う方法は、ボルトが複数本の場合には無理があり、接触要素を使った有限要素法解析が必要になるというのが筆者の見解です。