「ねじ締結体」を理解する：CAEを正しく使い疲労強度計算と有機的につなげる（14）（2/4 ページ）

金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第14回では、本連載の2つ目の本丸である「ねじ締結体」について取り上げる。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

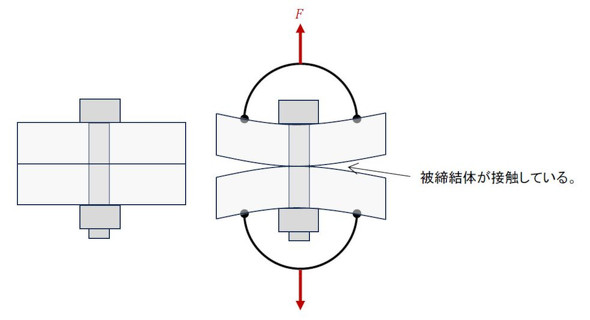
　では、図5に示すようにボルトがあるトルクで締結されていた場合を考えます。ボルトには軸力が発生しているので、被締結体は接触した状態を維持します。上の被締結体と下の被締結体との接触部には何らかの力のやりとりがあります。

図5　あるトルクで締結された締結体に繰り返し荷重Fが作用している状態［クリックで拡大］

　締結体が分離しない場合のボルトに発生する応力振幅は式7で表されます。σ_a0は式4で示した「荷重÷断面積」です。

式7

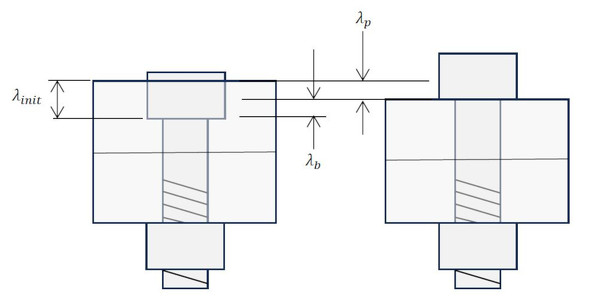
　式7のφは0.1〜0.2［-］くらいの値で「内力係数」と呼びます。では、内力係数を求めましょう。図6において、ボルトを例えば20［deg］回転して締め付けたとします。図6左図はボルトが回転によってλ_initだけ進んだ状態です。ボルトと被締結体は干渉するのでこのようにはならずに、ボルトがλ_bだけ伸びて、被締結体がλ_pだけ縮んで図6右図のようになります。

図6　ボルトによる締結状態：初期状態［クリックで拡大］

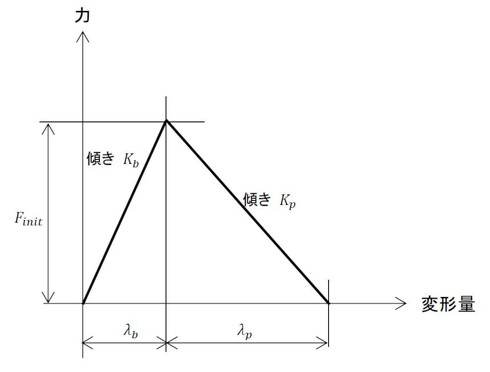
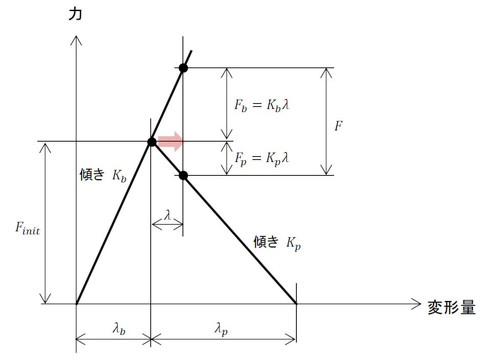
　ボルトが被締結体を押す力と被締結体がボルトを押す力は等しいので、力と変形量の関係を図7のように表すことができます。横軸が変形量で縦軸が力なので、この線の傾きはばね定数になります。実は、被締結体のばね定数の方が圧倒的に大きく傾きが急になるのですが、説明しやすいように傾きを緩くしてあります。この図から式8が成立します。

図7　締結体力と変形量の関係：初期状態［クリックで拡大］

式8

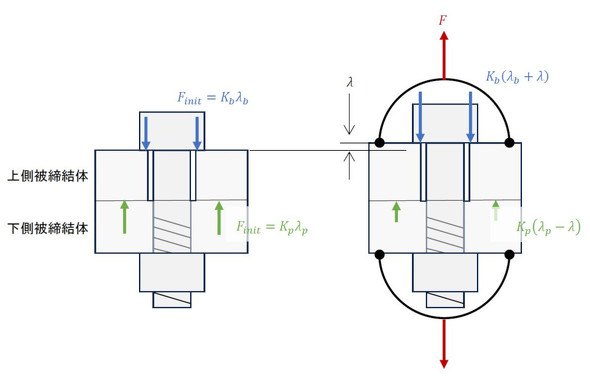
　図8に、荷重が作用する前後の状態を示します。荷重が作用したときのボルトと被締結体の変形量（伸び量と縮み量）は等しくλとなります。ボルトと被締結体の変形量が変わったので、ボルトが上側被締結体を押す力と下側被締結体が上側被締結体を押す力が変わります。

図8　ボルトによる締結状態：荷重状態［クリックで拡大］

　図8右図の状態で、上側被締結体に作用する上下方向の力のつり合い式を作りましょう。式9となります。

式9

　式8を使うと、λは以下となります。

式10

式11

　ボルトが上側被締結体を押す力はF_init（K_bλ_b）からK_b（λ_b＋λ）に変わりました。この変化量F_bは式12になります。

式12

　式12に、式11を代入します。

式13

　前述した力と変形量の関係を図示したものを図9に示します。ボルトの文献でよく見る図ですね。

図9　締結体力と変形量の関係：荷重状態［クリックで拡大］

　ボルトが上側被締結体を押す力の変化量F_bに注目します。これをねじ部の有効断面積A_Sで割り、その半分がボルトに発生する応力振幅で式14となります。

式14

　ボルトが締め付けられていなかったときの応力振幅は式4でした。式4を式14に代入します。

式15

　式15と式7を見比べると、内力係数φは式16となります。

式16

　ボルトが締め付けられていなかったときの応力振幅（これは「荷重振幅÷断面積」の半分です）を、φ倍したものがボルトが締め付けられているときの応力振幅となります。

　ここで余談ですが、繰り返し荷重が作用し続けている状態を考えます。最初はボルトが締め付けられているので応力振幅は小さく、疲労破断しなかったとします。次に、ボルトが緩んだとします。ボルトに作用する応力振幅は1／φ倍、だいたい5倍となるので条件が悪ければそのボルトは疲労破断します。ボルトの緩みと疲労破断は密接な関係があります。