オープンコレクタを用いたバス接続の有用性:今岡通博の俺流!組み込み用語解説(6)(1/2 ページ)
今岡通博氏による、組み込み開発に新しく関わることになった読者に向けた組み込み用語解説の連載コラム。第6回では、オープンコレクタを用いたバス接続の有用性について説明する。
はじめに
今回は、前々回の連載第4回で紹介したオープンコレクタの続編記事になります。まずは連載第4回を読んでオープンコレクタの基礎を振り返っていただくのがお勧めです。
連載第4回では、オープンコレクタがマイコンと外部機器の接続で重要な役割を果たすことを説明しました。今回は、オープンコレクタを用いたバス接続について解説します。これは、次回以降に取り上げる予定の「I2C(Inter-Integrated Circuit)」の前振りにもなっていたりします。
筆者の今岡氏が「Open Source Conference 2024 Hiroshima」に登壇!
広島で開催されるオープンソースの祭典「Open Source Conference 2024 Hiroshima」の講演に、本連載筆者の今岡氏が登壇します。詳細は以下のイベントURL、講演概要のURLからご確認ください。
講演日時:2024年9月29日(日)16:00〜16:45
講演タイトル:今こそはじめてみようFPGA(初学者大歓迎)
会場:サテライトキャンパスひろしま(広島県民文化センター5F)
イベントURL:https://event.ospn.jp/osc2024-hiroshima/
講演概要のURL:https://event.ospn.jp/osc2024-hiroshima/session/1712836
なぜバス接続にオープンコレクタを使うのか
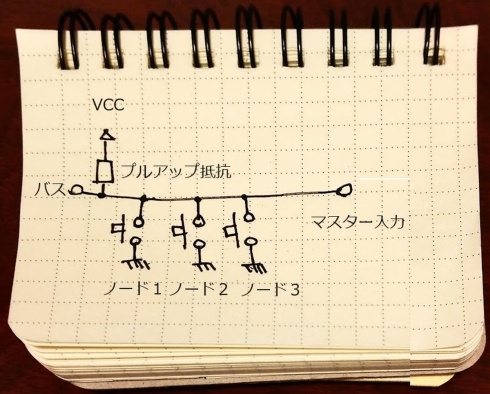
図1の回路は、単一の線(バス)に複数のノードがつながっています。これをバスモデルといいます。
それぞれのノードにNPN型のトランジスタを接続して、オープンコレクタの回路を形成する場合には、3つの電極であるエミッタ(E)、ベース(B)、コレクタ(C)のうち、コレクタがノード側につながります。また、エミッタ側はグランド(GND)に落とします。
これに対して、ノードに接続するのがNチャネルのFET(電界効果トランジスタ)の場合には、3つの電極はソース(S)、ゲート(G)、ドレイン(D)であり、ドレインをノード側につなげ、ソース側をグランドに落とすオープンコレクタと同様の回路はオープンドレインとなります。
ただし、図1では話を分かりやすくするためにタクトスイッチを使っています。NPN型トランジスタであればベースからエミッタに電流を流すとタクトスイッチは閉じた状態になります。一方、NチャネルのFETであればゲートに一定以上の電圧をかけると、タクトスイッチは閉じた状態になります。
バスの一方の端でプルアップ抵抗を介してプラス電源(VCC)につなぎます。そしてもう一方の端をマスター入力に接続します。
この接続の状態ではマスター入力の値は高電位すなわちVCCの電位になります。そこで、ノードのどこか1カ所でも閉じた状態にするとマスター入力の値は低電位、すなわちグランドの電位まで落ちます。
ただし、図1の回路だと複数のノードのタクトスイッチが閉じたとしても同様に低電位になるので、どのノードのタクトスイッチが閉じたかは区別できません。しかし実際のI2Cなどでは、各ノード間でデジタル的な信号をやりとりすることで特定できるようになっていますが、そのあたりについては割愛します。ここで議論したいのは、あくまでもアナログ的な電気回路の動作だからです。
押さえておきたいのは、単一のバスに複数のノードをぶら下げる場合は、解放とグランドの二値をとるドライブ回路が適しているということです。このドライブ回路がオープンコレクタだったりオープンドレインだったりするわけで、そのことを簡単に説明するために取りあえず疑似的にタクトスイッチを使いました。
そもそも、なぜ同一のバスに複数のノードを接続するバスモデルを取り上げたかというと、この方法以外ではマスターから各ノードに信号線を用意する必要があるためです。つまり、このバスモデルは信号線の数を圧倒的に削減できるので、プリント基板のフットプリントも小さく抑えることができます。これにより基板の面積を小さくできますし面積は同じでもプリント基板の積層数を削減できます。これは製品のコスト削減に大きく寄与しますよね。
Copyright © ITmedia, Inc. All Rights Reserved.