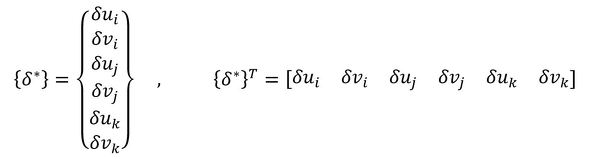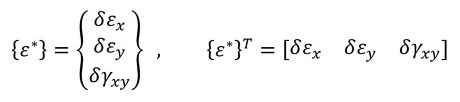有限要素法入門 〜要素剛性マトリクスの導出〜：CAEを正しく使い疲労強度計算と有機的につなげる（4）（2/7 ページ）

金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第4回は、前回に引き続き「有限要素法」について解説する。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

要素剛性マトリクスの導出

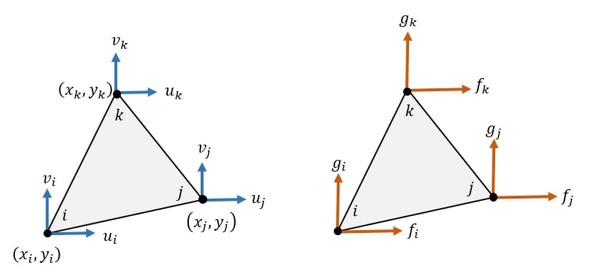
　では、要素剛性マトリクスを導出しましょう。2次元平面応力状態の要素に作用する力と変位を図3に示します。

図3　三角形要素に作用する荷重と変位［クリックで拡大］

　変位ベクトル、荷重ベクトル、剛性マトリクスで表すと次式となります。

式10

式11

　次に、仮想変位ベクトル｛δ^*｝と仮想変位によるひずみベクトル｛ε^*｝を次式で定義しましょう。ベクトルの肩に付いている「T」は転置行列という意味です。

式12

式13

式14

　応力ベクトルは次式でした。

式15

　図3に示すように外力は節点への集中荷重なので、式9-2Dの第1項の積分は次式となります。

式16

　体積力はないものとして式9-2Dの第2項は無視します。式9-2Dの第3項は式14、式15を代入すると次式となります。

式17

　式16、式17から式9-2Dは次式となります。

式18