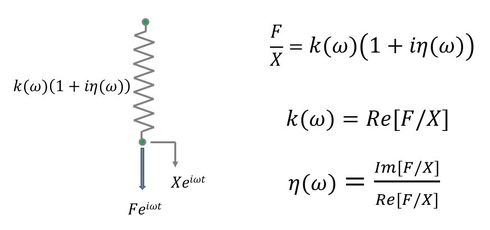ランドリー（洗濯機）を題材に音振動の低次元化モデリングを考える：1Dモデリングの勘所（8）（2/3 ページ）

「1Dモデリング」に関する連載。連載第8回では音振動のモデリングの事例として、ランドリー（洗濯機）を取り上げる。まず、ランドリーとは何かを機能と構造の視点で考える。その後、音振動の伝達経路、ランドリー固有の要素を説明し、ランドリーの1D振動モデルを示す。また、振動数が変化する外力のモデリング方法とゴムのモデリング方法を紹介する。これらを踏まえ、ランドリーの振動モデルを構築、定式化、解析し、最後に音の1Dモデリングに言及する。

[大富浩一／日本機械学会 設計研究会，MONOist]

振動数が変化する外力のモデリング

　外力の振動数が一様に変化する場合の表現方法について考える。“外力の振動数が一様に変化する”とは、「角加速度が一定値である」ということなので、位相をΦとすると、角加速度は、

式1

と表現できる。ここに＋のとき「昇速」、−のとき「減速」となり、εは昇降速の速さを表現する正の定数である。上式から、外力の角振動数および位相は、

式2

式3

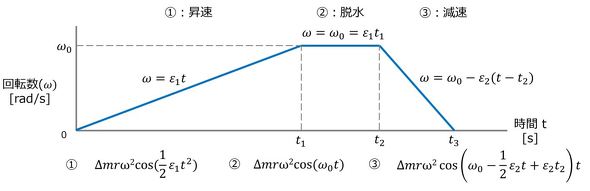
となる。ここに、ωは初期状態の角振動数、αは位相角である。上記の知見を基に、脱水時回転槽の回転数変化を表現すると図6となる。すなわち、静止状態から、角加速度ε₁、角速度ε₁tで昇速、所定の回転数ω₀で脱水、その後、角加速度−ε₂、角速度ω₀−ε₂（t−t₂）で減速する。ここで、時刻0からt₁までが昇速、t₁からt₂までが一定回転、t₂からt₃までが減速区間である。各区間の外力は図6下部に示すように表現される。

図6　脱水時回転槽の回転数変化の表現［クリックで拡大］

粘弾性体（ゴム）のモデリング

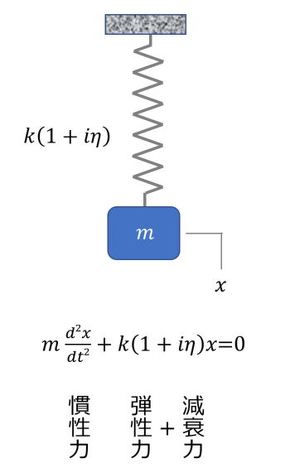
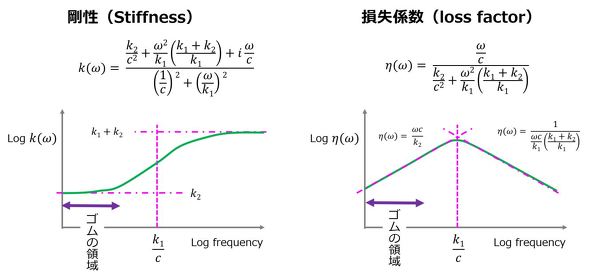
　ゴムは、防振材料として使用されることが多い。これは良好な減衰特性を有するためであるが、一方で通常の金属材料とは異なり、モデリングが容易ではなく、さまざまな試みが行われている。すなわち、ゴムはいわゆる粘弾性体で、材料自体が剛性と減衰特性を有する。そこで、一般には図7に示すように複素数剛性で表現される。ここで、kが剛性に関するもので、ηが損失係数と呼ばれ、減衰に関するものである。また、粘弾性ばねの場合には、剛性も損失係数も周波数ωの関数となるため、図8のように定義される。

図7　粘弾性ばねで構成される振動モデル［クリックで拡大］

図8　粘弾性ばねの定義［クリックで拡大］

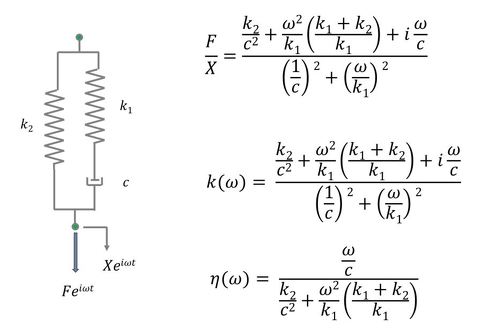
　粘弾性ばねのモデリング方法として、ばね要素と減衰要素を組み合わせた図9の粘弾性ばねモデルが使用される。このように、2種類のばね要素、減衰要素、振動数を用いて、剛性と損失係数を表現できる。図9の剛性と損失係数を横軸に、振動数をとって示すと図10のようになる。実験などにより、ゴム材料の剛性、損失係数を把握し、これを表現するように2種類のばね要素と減衰要素の値を定義することになる。

図9　ばね要素と減衰要素の組み合わせによる粘弾性ばねモデル［クリックで拡大］

図10　粘弾性ばねのモデリング例［クリックで拡大］