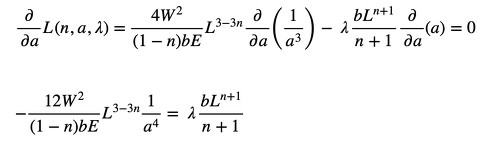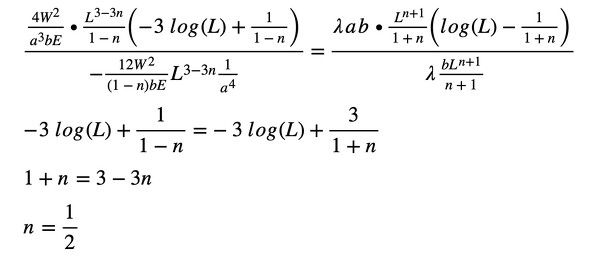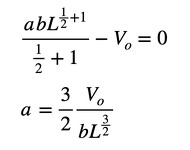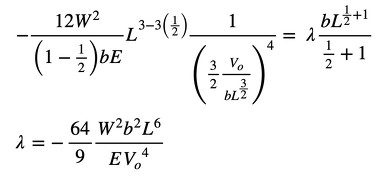剛性を最大化するはりの形状を求める：フリーFEMソフトとExcelマクロで形状最適化（3）（2/3 ページ）

原理原則を押さえていれば、高額なソフトウェアを用意せずとも「パラメトリック最適化」「トポロジー最適化」「領域最適化」といった“形状最適化”手法を試すことができる！　本連載ではフリーのFEM（有限要素法）ソフトウェア「LISA」と「Excel」のマクロプログラムを用いた形状最適化にチャレンジする。連載第3回では、片持ちはりの平均コンプライアンス最小化問題を「ラグランジュの未定乗数法」を使って解いていく。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

平均コンプライアンスを最小化、剛性を最大化するはりの形状

　それでは、ラグランジュの未定乗数法を使って、平均コンプライアンスを最小化、つまり剛性を最大化するnとaを求めましょう。

　ラグランジュ関数L（式4）は次式となります（式15）。

式15

　式5を計算しましょう（式16）。

式16

　第1項のL^3-3nの微分は以下のようにします（式17）。

式17

　両辺を微分します（式18）。

式18

　2つの関数の商の微分公式は次式でした（式19）。

式19

　よって、式16は以下のようになります（式20）。

式20

　「こんな微分は学生のときにやって以来で、社会人になって初めてだ！」という方もおられると思いますが、少しお付き合いください。

　式6を計算しましょう（式21）。

式21

　式20を式21で割り算します（式22）。

式22

　n＝1／2となりました。式1は次のようになります（式23）。

式23

　あれ、どこかで見た式ですね。“平等強さのはり”と同じ結果となりました。平等強さのはりは、剛性最大のはりでもありました。こんなことは材料力学の講義では習いませんでした。筆者も本連載を書きはじめて知りました。

　では、aを求めましょう。

　式3に式23を代入します（式24）。

式24

　λを求めましょう。式21に式23、式24を代入します（式25）。

式25