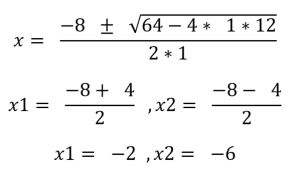テストでバグ発見！（4）懐かしい「解の公式」のプログラムからバグを探し出せ：山浦恒央の“くみこみ”な話（146）（1/4 ページ）

提示された仕様とプログラム（バグを含む）から、自身の手でテストケースを設計し、バグを実際に見つけ、バグレポートまでを作成する実践的なシリーズ「テストでバグ発見！」。第4回は、多くの読者が中学校の数学で学んであろう、2次方程式の解を求める「解の公式」のプログラムに潜むバグを見つけ出そう。

[山浦恒央 東海大学 大学院 組込み技術研究科 非常勤講師（工学博士），MONOist]

※本記事はアフィリエイトプログラムによる収益を得ています

1．はじめに

　このシリーズは、筆者がバグを仕込んだ要求仕様とプログラムを基に、テスト設計してバグを見つけるものです。今回は、2次方程式の解を求めるプログラムを題材としました。自分なりのテスト項目を作成し、バグを見つけてください。

⇒連載「山浦恒央の“くみこみ”な話」バックナンバー

2．コンピュータと数値演算

※写真はイメージです

　コンピュータは、プログラムを作成すれば、短時間ではできない計算を超高速で実行します。例えば、人間は「154×983の結果は幾つですか？」と聞かれると、「えーと……」と思考停止します。一方、コンピュータは、人間が正しくプログラムを作成すれば、一瞬で計算できますね。

　現在の社会は、さまざまなコンピュータの計算能力によって成り立っており、そこにバグがあると、社会生活に大きな影響を及ぼします。

　今回は、数値演算の題材として、2次方程式の解を求める手法である「解の公式」を題材とします。今回は、すぐにバグが見つかると思いますので、チャレンジしてみてください。

3．【問題】解の公式算出プログラム　制限時間：90分

　下記に示す仕様および提示するプログラム（Python）からテスト項目を作成し、バグを検出せよ。また、バグを検出した場合は、バグレポートにまとめること。

• 提示物：問題のプログラム（QuadraticEquation.py）:Python3.9.5で確認済み（Windows）
• 成果物：記述済みのテスト項目、記述済みのバグレポート

⇒QuadraticEquation.pyのダウンロードはこちらから

※1）使用するWebブラウザや設定によって、上記のリンクをクリックしてもソースコードが文字化けした状態で表示される可能性があります。その場合は、右クリックメニューから「名前を付けてリンクを保存」を選ぶことによってファイルをダウンロードできます。また、ダウンロードしたファイルが開けない、または、セキュリティの観点からWebサイトからファイルをダウンロードして開きたくない場合、記事末付録のソースコードのテキストをコピーして使用してください。なお、文字化けする場合は、utf-8で開いてください。

3.1 概要

　問題にチャレンジにする前に、解の公式の概要を説明する。

　2次方程式とは、「ax²＋bx＋c＝0」のように、次数が2の方程式である。中学や高校で習ったことがあるはず。2次方程式の解を求める方法には、「因数分解」「解の公式」などがある。

　因数分解とは、足し算や引き算で表現した式をかけ算の形にすることである。例えば、x²＋8x＋12＝0という式があれば、「（x＋2）（x＋6）」の形に変換し、解として、x＝−2、x＝−6を求める。

　因数分解はうまくいく場合が多いが、分数や無理数が入ると難しくなる。その時は、解の公式を使用する。解の公式では、2次方程式のa、b、cを以下の式に入れることで、解を算出できる（a≠0の場合）。

　例えば、x²＋8x＋12＝0を解の公式で解く場合、a＝1、b＝8、c＝12として、上の式に代入し、結果を算出する。

　結果として、x1＝−2、x2＝−6という解を求めることができる。

　2次方程式には、a、b、cの値によって、解の数が異なる（「2つの異なる実数解」「重解」「解なし」）となる。そこで、事前に解が数を知りたい場合は、下記の判別式の結果を表すDから解の数を把握する。

　判別式Dを計算すると、「D＞0の場合は、2つの異なる実数解」「D＝0の場合は、重解」「D＜0の場合は、解なし」となる。