連載
バグ検出ドリル(6)いろんなところにバグがいる! 2分探索法の問題:山浦恒央の“くみこみ”な話(106)(2/4 ページ)
「バグ検出ドリル」の第6回で出題するのは「2分探索法」の問題です。ソフトウェア技術者の誰もが心得ておくべき常識的なアルゴリズムである2分探索法ですが、今回の問題では、いろんなところにバグがあります。問題文から、どこにバグがありそうか見つけ出してみよう!
3.例題を基にした2分探索法のイメージ
無駄を省く手法の1つが、「2分探索法(binary search)」というアルゴリズムです。2分探索法は、検索するデータが中央値より高いか低いかを判断して探索します。なお、検索する配列の中身は、ソートしてあることが前提です。リスト1の配列を参考に、手順を示します。
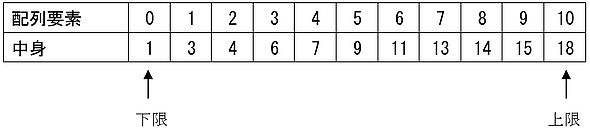
手順1:配列の探索範囲の下限(low)と上限(high)をセットします。例題では、左側が「0」で、右側が「10」ですね。
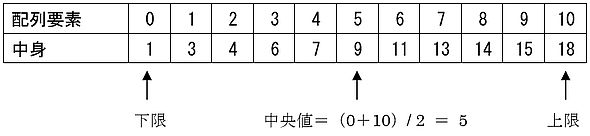
手順2:中央値(mid)の配列要素を算出し、下限≦上限が成立する間、繰り返します。つまり、中央値とは、下限と上限の配列要素を足し、2で割った値です。リスト1で、1回目は下限の配列要素が「0」、上限が「10」なので、中央値は(0+10)/2=5となります。
上記の計算を、「下限≦上限が成立する間まで繰り返す」、すなわち下限>上限となったら終了です。探索を続けていくと、下限と上限の関係が逆転するタイミングが現れます。
手順3:下記の3つのステップで、検索処理を実施する。
- ステップ1:中央の配列の中身が、検索したい数字と同じ場合、検索終了です。リスト1において、見つけたい数字が、「9」の場合は、1回目で終了となります。
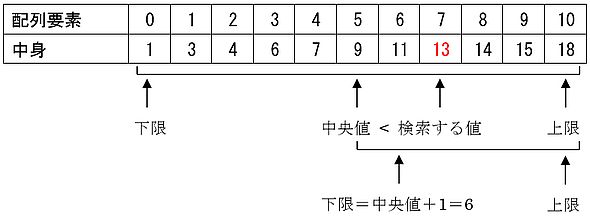
- ステップ2:「検索する数値>中央値の配列の中身」の場合は、中央値の配列要素より前に小さい数値が無いと分かります。よって、下限の配列要素=中央値の配列要素+1とし、手順2に戻ります。例えば、探したい数値が「13」、中央の中身が「9」の場合は、9より小さい値を見る必要がありませんから、「下限の配列要素=5+1」とし、手順2に戻ります。
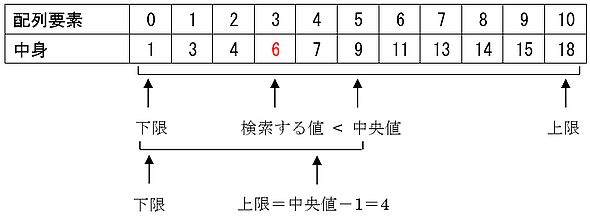
- ステップ3:「検索したい数値<中央値の配列の中身」の場合、中央値から先に、大きい数値が無いと分かります。よって、「上限の配列要素=中央の配列要素−1」とし、手順2に戻ります。例えば、探したい数値が「6」、中央の配列の中身が「9」の場合は、9より大きい値は見る必要がありませんから、「上限の配列要素=5−1」とし、手順2に戻ります。
目的とするデータにヒットしなかった場合、「上限の配列要素」や「下限の配列要素」を1つ加算、減算して、少しでも早く見つかるようにしているのかミソです。大体のアルゴリズムが分かったと思います。では、実際に問題に取り組みましょう。
Copyright © ITmedia, Inc. All Rights Reserved.