「図面から加工方法を察してみよう」の巻：ママさん設計者がやさしく教える「図面の読み描き超入門」（4）（1/3 ページ）

図面にも触れたことのないような初心者を対象とした、図面の読み方・描き方講座。お題をクリアしながら、解説を読み進めていくことで、いつしか図面の読み描きができるようになる！ 今回は「加工方法の察し方」をテーマにお題と解説をお届けする。

[藤崎 淳子／Material工房・テクノフレキス，MONOist]

　皆さんこんにちは！

　前回の「『形体をコントロールする方法を覚えよう』の巻」では、「幾何」「データム」という聞き慣れない単語や記号がたくさん登場したことで、これまでの記事に比べると難易度が一気にアップしたな……と感じられたかもしれません。

　しかし、モノづくりの世界で実際に飛び交う図面というのは、形状と寸法数値だけでは必要な要素の全てを伝え切れません。少なくとも「幾何公差が、どんなときに使われるものか」を知っておくことで、図面を手にしたときにそれが何を示しているのか理解でき、図面の全容をつかむことができると思います。

　本連載の狙いは、“図面を読むこと”に慣れることです。そして、“一から図面を描くこと”への動機付けです。ですから、「超入門」らしく、基礎的な内容を中心とし、初心者向けに要点を絞って分かりやすく解説していきますので、引き続きよろしくお願いします。

宿題の解答と解説

　まずは、前回の宿題の解答からスタートしたいと思います。

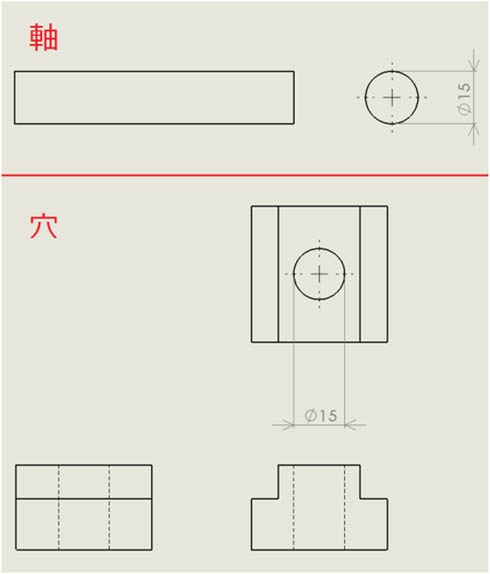
　前回の宿題は、「軸が穴に真っすぐ入ってスムースにフィットするように、軸も穴もシャキッとキメてください。公差値は、0.01でお願いします！」というごちゃごちゃとしたメッセージを解読して、幾何公差を図面に記入するというものでした。

　まず、このメッセージから重要な要素を読み取ってみましょう（図1）。

図1　前回の宿題で提示した図面　※画像クリックで拡大表示

　ヒントは「カーブ禁止」でした。つまり、軸も穴も「曲がってはいけない」のです。ということは、メッセージの中の「真っすぐ入って」が、最も重要な要素と考えられます。これを踏まえ、まず「形状公差」の中から「真っすぐ」に有効な幾何公差は何かを検討します（前回掲載した「幾何公差一覧表」から、形状公差の部分を抜き出しましたのでご参照ください）（図2）。

図2　「幾何公差一覧表」の抜粋　※画像クリックで拡大表示

　候補としては、

• 真っすぐさを表す「真直度」

が考えられますね。

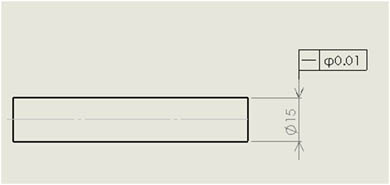
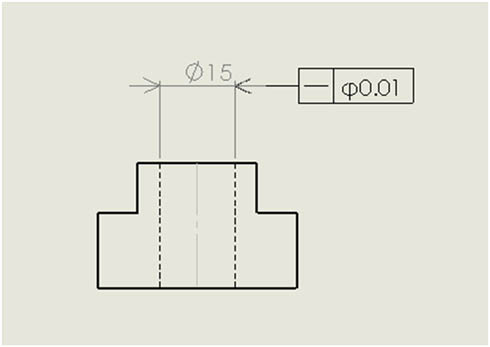
　「真っすぐ入る」「曲がってはいけない」のであれば、軸線に真直度を指示することで狂いを抑えることができます。つまり、前回の宿題の正解は、ヒントから導き出した「真直度／φ0.01」となります（図3、図4）。

図3　前回の解答（1）　※画像クリックで拡大表示

図4　前回の解答（2）　※画像クリックで拡大表示

　今回の宿題で、同時に注意しておきたいフレーズが「スムースにフィットする」です。これをモノづくり用語っぽく表現するなら、「干渉せずスキマなくはめ合うこと」でしょうか。そのために有効な幾何公差の候補としては、

• どれだけ真円に近いかを表す「真円度」
• どれだけ円筒に近いかを表す「円筒度」

が考えられます。しかし、この2つ……何だか似ていますよね？

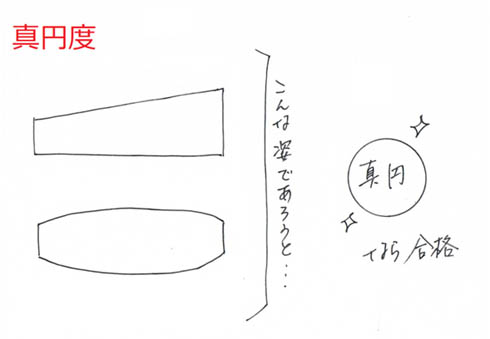
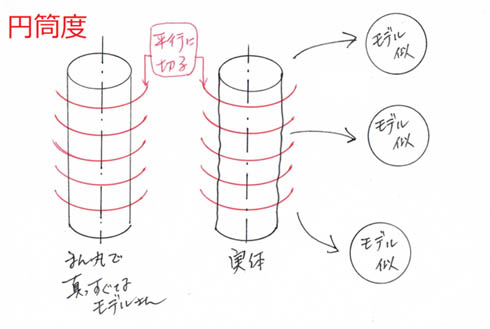
　この少々紛らわしい円筒度と真円度の違いを分かりやすく説明すると、対象の形体そのものが真っすぐでなくても（メガホンのような円すい状や和太鼓のように膨らんだ形状であっても）、輪切りにしたときの断面が、指示された公差内の真円であればOKなのが真円度です（図5）。

図5　「真円度」について　※画像クリックで拡大表示

　対する円筒度は、“真円で真直なモデルさん”を想定して、実体をそれに合わせて平行に切ったときに、指示された公差内の“モデルさん”と同じ真円が出てくればOKです（図6）。

図6　「円筒度」について　※画像クリックで拡大表示

　このように、口ではカンタンには言えますが、現場の加工者にとっては、真円度よりも円筒度を指示される方がはるかに大きなプレッシャーとなります。なぜなら、円筒度というたった1つの幾何公差を実現するために、真直度、真円度、平行度（先端から終端までの径のバラツキ）といった複数の幾何公差を確認しながら加工を進める必要があるからです。

　この円筒度は、加工者にとって手間の掛かるものですが、真っすぐ入るだけでなく「スムースにフィット」まで考慮する場合には、非常に有効な指示となります。

　ただし、宿題にあるごちゃごちゃとしたメッセージだけでは、円筒度まで指示すべきかどうか判断しかねるので、こういう場合は独断で幾何公差を増やさないで、発言者に設計意図を確認した上で、誤解やムダな工数を生まない図面を描くようにしましょう。