変化のない人生と伝達関数は、あり得ない？：独学！ 機械設計者のための自動制御入門（7）（4/4 ページ）

時間が十分経過したときの伝達関数の特性は、周波数応答特性で見れば低周波領域の特性に対応しているのはなぜ？

[岩淵 正幸／技術士（機械部門），MONOist]

ほめるのは最後まで聞いてからにしてよ。直線のセンターライン上を走っていたら、突然横風が吹いて車が横ずれするんだったね。つまり入力値Xに変化はない。横風による操舵角の外乱δがあってもフィードバック制御だから、その影響を受けずに目標位置Xの上を車は走って欲しい。そうなるかどうかはt⇒∞のときの外乱δの影響の有無を調べればいい

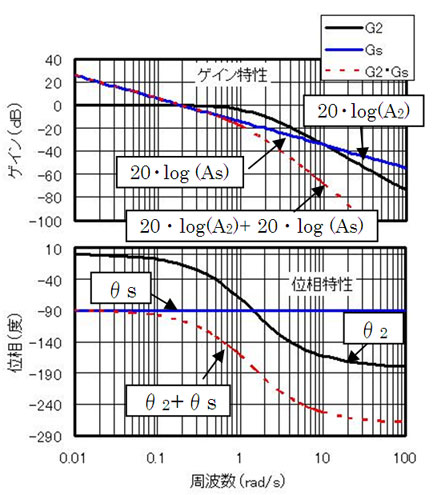
それは周波数領域でいえばω⇒0のときの特性を調べることに相当する。そこで、前ページの図6・7の周波数応答特性をみると、ω⇒0では、GoもGsも、ゲインは∞だ。従って……

ω⇒0で……

がどの程度小さくなるかで、風外乱δの影響の大きさが異なってくる

そうや。もう少しや

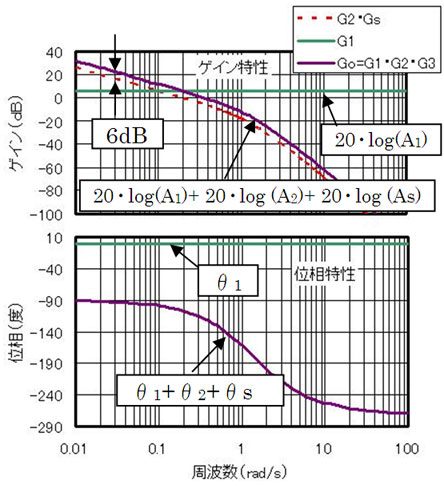
それで、図6と図7から、ω⇒0におけるGoとGsのゲインの差をみると、Goの方がGsより6（dB）大きい。これを振幅比に直すと

ここまでは、いままでの復習だな

さて、ここからが本番だよ。制御対象Gsの特性は変えられないからコントローラG1の特性を変えることになる。まず、G1を比例要素ではなく、積分要素に置き換えるとどうなるか考えてみると……

浴槽の水位制御を思い出せば、どうなるか簡単に分かるやろ……

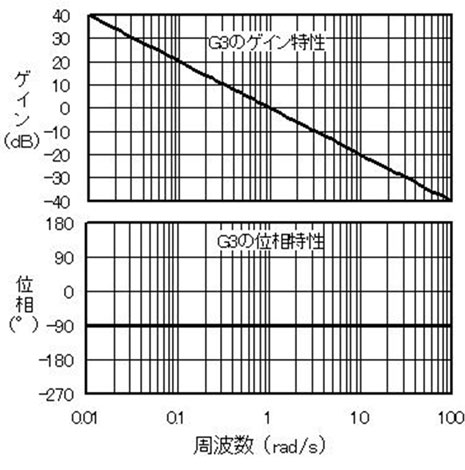
G1を積分要素にすると、図8に示すようにω⇒0でゲインは∞となる。つまりG1⇒∞だ。一方、G2は図6からω⇒0でG2⇒1。従って……

図8　積分要素のボード線図

このあたりは、浴槽の水位制御とまったく同じだな

だから、G1を積分要素にすると、外乱、つまり風の影響をなくすことができる。従って、強風が吹いても車はセンターラインの上を走ることができる。しかし、G1を積分要素にすると、その位相曲線は図8に示すように−90°だね。すると図7の開ループ伝達関数Goの位相曲線は、90°下に下がるから、−180°〜−360°の範囲に移動する。これはどう見たって不安定になってしまう

そうや。そこで……

浴槽の水位制御と同様に、G1を比例＋積分にしてみる……その伝達関数は、前回の浴槽の水位制御と同様に、比例要素の係数をc、積分要素の係数をbとすれば伝達関数は……

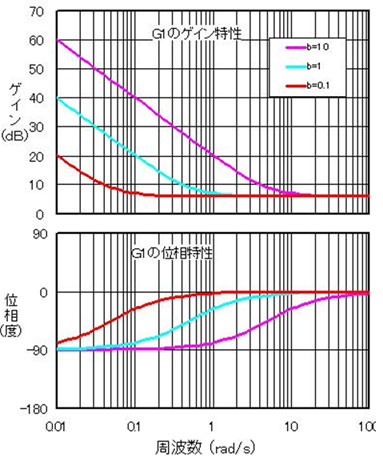
比例制御の比例定数cを2（°/m）として、b（°rad/s/m）をパラメータとしてExcelを使ってG1の周波数応答曲線を書くと図9のようになる。これらに対して、開ループGoのボード線図を描くと図10になる

図9 （比例＋積分）要素のボード線図

図10 （比例＋積分）制御の開ループ伝達関数のボード線図　

図10で位相余裕あるいはゲイン余裕を調べると……b＝0.1以外は、安定性に余裕がないからアカンな

そうだね。結局、横風が吹いても、横ずれしない自動走行制御システムのブロック線図は図11のようになる

図11 横風を受けるときの自動走行制御構成

草太！ よくできたな!! ところで、制御器が、比例＋積分の要素から構成される制御システムをなんていうか、知っとうか？

知らない

比例のProportionalのP、積分のIntegralのIをとって、PI制御って呼ぶんだ。覚えておきよ

分かった

　動画1は、P制御のみの場合のシミュレーション結果です。横風を受けて、車が0.5mずれるのが分かりますね。動画2は、積分補償を加えてPI制御としたときのシミュレーション結果です。確かに、横風を受けて車がずれても元の位置に戻ろうとはしています。しかし、思ったほど改善されているとは思えません。何かが足りない気がします。

動画1 比例制御

動画2 比例＋積分

◇

　次回は、動画2における問題点を探りながら、動特性改善の話に移ります。

Profile

岩淵正幸（いわぶち まさゆき）

1953年生。技術士（機械部門）。日本セメント（現太平洋セメント）、川崎重工業精機事業部（現カワサキプレシジョンマシナリ）を経て、現在事務処理機器メーカーでシミュレーションを活用した設計方法の開発および設計コンサルティング業務を担当。川崎重工では、油圧制御システム設計、旧石油公団（現石油天然ガス・金属鉱物資源機構）委託研究による圧力波通信システムの開発研究、対戦車用ミサイル操舵装置の開発に従事。

*** 一部省略されたコンテンツがあります。PC版でご覧ください。 ***