幾何公差の相互関係は、F<O<L:製図を極める! 幾何公差徹底攻略(10)(1/2 ページ)
今回は、いよいよ最終回。幾何公差同士の相互関係について整理して、ロジカルに指定しよう。
前回までに、設計意図を表す寸法記入方法から始まり、加工によってカタチがばらつき、計測によって曖昧さが発生することを知りました。また、幾何公差の基本であるデータムの記入法や領域の把握、4つのグループに分かれる幾何公差についても説明してきました。
寸法公差と幾何公差の関係
寸法公差は大きさを制御する場合に指示し、形の崩れ(そりやうねり、位置ずれ)を制御する場合は幾何公差を指示します。なぜ幾何公差が必要なのかというと、寸法や寸法公差ではどうしても伝え切れない形状があるからです。
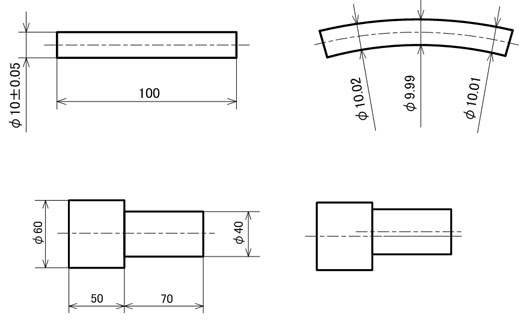
図1を見てください。
そりが極めて小さく、かつ真っすぐな軸を設計者が要求する場合、寸法公差を極限まで厳しい数値に変更しても軸のそりについて指示することはできません。寸法はあくまでも2点間測定なので、2点間の直径寸法さえ満足すれば合格となり、そりというカタチの崩れを検査できないのです。同様に、段付き軸の場合、直径の異なる複数の形体の同軸をうたいたくても、寸法線で「0」を記入できないため、表現する手段がありませんでした。
そこで幾何公差が登場し、そりや同軸のずれがいくらまで許されるのかを指示するわけです。寸法公差と幾何公差は互いに関連を持たないという関係があり、それが、これまでの回でも何度か出てきた独立の原則です。
独立の原則:単独形体、つまり円筒面または平行2平面によって決められる1つの形体(サイズ形体)に対して適用する。この条件は、形体がその最大実体寸法における完全状態の包絡面を超えてはならない。
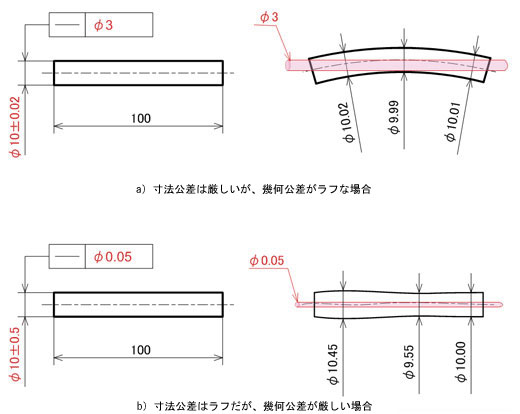
へ理屈になってしまいますが、独立の原則から図2のように解釈することが可能です。
特に指示がない限り、JISでは独立の原則を採用しますが、逆の考え方も存在します。
つまり、「寸法公差と幾何公差を一緒に考えましょう」というもので、「包絡の条件」といいます。包絡の条件は、一般的に長さ寸法の後に記号「E」を付記します。包絡という言葉は、イメージがつかみにくく、国語辞典で調べても解釈が難しい言葉です。
この「E」は、「Envelope(=封筒)」の頭文字を取ったもので、「包絡の条件が指示された部品にそりやうねりがあっても、寸法公差の最大値で作った封筒の中に入ればOK」と理解すればイメージしやすいと思います。
包絡の条件:単独形体、つまり円筒面または平行2平面によって決められる1つの形体(サイズ形体)に対して適用する。この条件は、形体がその最大実体寸法における完全状態の包絡面を超えてはならない。
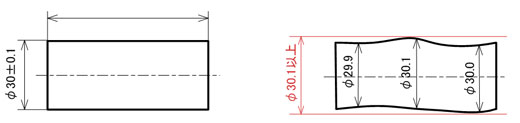
独立の原則の下で寸法公差を指示すると、その形体の存在できる物理的な範囲は、最大寸法より大きくなります(図3)。
上記のような独立の原則を適用する場合、加工者は寸法公差のど真ん中を狙うことが一般的であると思います。
これに対して、包絡の条件を適用した場合、寸法公差は満足したうえで、寸法公差で示された最大実体状態(軸の場合は最も大きくなる状態、穴の場合は最も小さくなる状態)の範囲内にその形体があるならば、カタチは崩れてもよいという考え方になります。
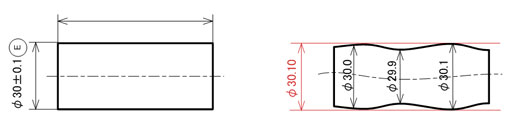
そのため、形体が最大実体寸法(軸の場合は公差の最大寸法、穴の場合は公差の最小寸法)で出来上がった場合、カタチの崩れは許されないことを意味します(図4)。
上記のような包絡の条件を適用するときに、ある程度そりやうねりが発生することは避けられないと判断した場合、加工者は寸法公差のど真ん中より少し小さ目を狙うことになると考えられます。
以上で、寸法と幾何の関係について整理しました。次のページでは幾何公差同士の相互関係について説明します。
Copyright © ITmedia, Inc. All Rights Reserved.