OpenGL ESプログラミングで本格3D描画体験：“BREW”アプリケーション開発入門（7）（2/3 ページ）

OpenGL ESによる3Dグラフィックス描画プログラミングに挑戦！ 投影、ライトなどの各種要素を理解し、立方体の描画を行ってみよう。

[末永貴一（エイチアイ），＠IT MONOist]

投影とは

　3Dデータの準備が終わりましたので、次にこの物体を3Dグラフィックスとして表示するための環境を設定します。前回は、特にこのようなことを意識せずに単に三角形の形状を指定して描画しただけでしたが、今回はこの部分をもう少し詳細に設定したいと思います。

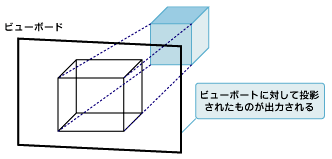
　そもそも、3Dグラフィックスとはコンピュータの中で描画対象である3次元データを計算し、それをグラフィックスとして画面に描画するものです。しかし、最終的な出力先であるディスプレイなどの画面は平面なので、出力時には2Dに変換する必要があります（ホログラフのような物理的に立体物を投影できるデバイスがあれば別ですが……）。この3Dグラフィックスが投影される2D面の矩形領域を「ビューポート」といいます。

図7　ビューポート

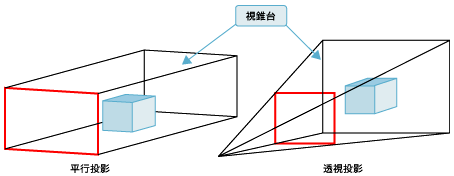
　この最終的に行われるビューポートに対しての投影の以前に、3D空間をどのように投影するのかを選択する必要があります。これにより、最終的な見え方が変わってきます。OpenGL ESでは「平行投影」と「透視投影」と呼ばれる投影方法を2つ用意しています。

　一般的に、平行投影は2Dに投影される3Dオブジェクトの辺の長さや面積が対象物と同じになり、空間上の遠近感はなくなります。それに対して、透視投影は3Dオブジェクトを人の目で見るのと同じように2Dに投影するため、遠近感が反映されます。

　平行投影、透視投影は用途によって使い分けることになりますが、3Dらしい空間や物体を表現するゲームなどには透視投影が用いられ、対象物の形状を正確に把握する3D CADなどに平行投影が用いられる傾向があります。いずれにせよ最終的にどのように3Dデータを見せたいかによって、投影方法が決まることになります。

図8　平行投影と透視投影

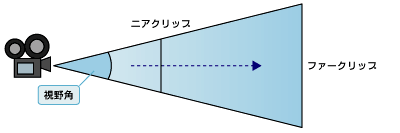
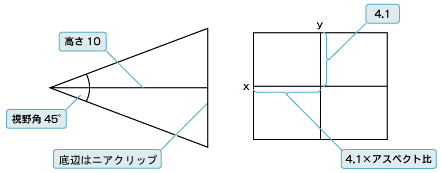
　各投影方法で実際の投影面になるのが、上記図8の赤い枠の面となります。具体的な説明はプログラムの中で解説しますが、前面の「投影面（ニアクリップ）」と、その後ろにある「背面（ファークリップ）」の間が3Dの描画対象となる3D空間ということになり、この部分を「視錐台（視体積）」といいます。

　投影面に映った状態は、最終的にビューポートに変換され、画面出力が可能になります。投影方法は、プログラム中で指定できますが、今回はより3Dらしい表示を行うということで、透視投影で3Dを表示したいと思います。

　視錐台を考える際に、もう1点留意する必要があるのが“カメラ位置”です。3Dグラフィックスにおけるカメラとは、いわゆる“視点”であり、3Dグラフィックスをどこから見ているかの基準となります。例えば、透視投影の場合、三角錐の頂点となる部分がカメラ位置となり、三角錐の底辺に向けて視線があるという感じになります。

図9　透視投影の場合のカメラ位置

　これらの各プロセスが、最終的な画面への描画に至る一連の変換処理となり、これを「レンダリングパイプライン」といいます。この一連の変換処理であるレンダリングパイプラインを簡潔にまとめると以下のようになります。

頂点情報→モデルビュー変換（3Dオブジェクト、カメラ）→投影変換→ビューポート変換→描画

　レンダリングパイプラインは、3Dグラフィックスの基本でもあり、ポイントでもありますが、より詳細に分解するとほかにも多くの要素があります。この部分は現在もより高度なグラフィックの実現のために進化しています。

ライト

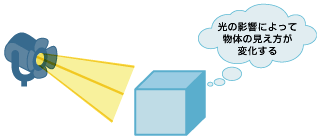
　3Dグラフィックスというと、どうしても立体的な表示が3Dであると思われてしまいますが、あくまで3Dグラフィックスは3次元の視覚的要素をグラフィックスで表現することです。このため、単純に物体を立体的に表示するだけだと、3Dグラフィックスの表現としては乏しいといえます。そこで、重要になるのが“光の影響”です。これは人の目が現実世界を見る際に、光の影響を大きく受けているからで、中でも“陰影”がリアリティを実現する重要な要素になります。3Dグラフィックスの陰影に関する技術はさまざまな要素があり、ここでは詳細は割愛しますが、OpengGL ESでは基本となる「環境光」「拡散光」「鏡面光」などのライト設定が可能になっています。

図10　光の影響

　それでは、以上を踏まえて、プログラムの内容を確認してみたいと思います。ここでは投影、ライトの設定、描画データの準備などを行います。

boolean setupGL(oes3d* pMe){
        GLfixed light_position[] = { -f16(5.0f), f16 (5.0f),
                                     f16 (5.0f), f16 (0.0f) };     //ライトの位置
        GLfixed light_diffuse[]  = { f16 ( 0.0f), f16 ( 0.0f),
                                     f16 ( 5.0f), f16 ( 0.0f) };   //青の拡散光
        float aspect;  // 画面アスペクト比
        // 画面設定
        ISHELL_GetDeviceInfo(pMe->a.m_pIShell, &pMe->DeviceInfo);  // 画面サイズ取得
        aspect = ((float)pMe->DeviceInfo.cxScreen / 
                 (float)pMe->DeviceInfo.cyScreen);  // 画面アスペクト比取得
        // 透視投影の設定
        IGL_glMatrixMode (pMe->m_pIGL, GL_PROJECTION);
        IGL_glLoadIdentity (pMe->m_pIGL);  // 行列の初期化
        // 投影面の中心から左X 座標, 右X 座標, 
           下Y 座標, 上Y 座標, ニアクリップZ 位置, ファークリップZ位置
        IGL_glFrustumx (pMe->m_pIGL, (GLfixed)(-f16(4.1f) * aspect),
                        (GLfixed)(f16(4.1f) * aspect),
                        -f16(4.1f), f16(4.1f), f16(10), f16(100));
        // ビューポート設定
        IGL_glViewport(pMe->m_pIGL, 0, 0, pMe->DeviceInfo.cxScreen,
                       pMe->DeviceInfo.cyScreen);
        // ライト設定
        IGL_glLightxv(pMe->m_pIGL, GL_LIGHT0, 
                      GL_POSITION, light_position);  // 照明の位置設定
        IGL_glLightxv(pMe->m_pIGL, GL_LIGHT0, 
                      GL_DIFFUSE, light_diffuse);    // 拡散光の設定
        IGL_glEnable(pMe->m_pIGL, GL_NORMALIZE);     // 法線正規化
        IGL_glEnable(pMe->m_pIGL, GL_LIGHTING);      // ライティング有効
        IGL_glEnable(pMe->m_pIGL, GL_LIGHT0);        // ライト有効
        // 背景クリアカラー
        IGL_glClearColorx(pMe->m_pIGL, f16(0.5f), f16(0.5f), f16(0.5f), f16(1.0f));
        //データ配列の有効化
        IGL_glEnableClientState (pMe->m_pIGL, GL_VERTEX_ARRAY);  // 頂点座標
        IGL_glEnableClientState (pMe->m_pIGL, GL_NORMAL_ARRAY);  // 法線 有効化
        // モデルビューの行列を用いる
        IGL_glMatrixMode (pMe->m_pIGL, GL_MODELVIEW);
        IGL_glLoadIdentity (pMe->m_pIGL);  // 行列初期化
        if (IGL_glGetError (pMe->m_pIGL) != GL_NO_ERROR){
                return FALSE;
        }
        return TRUE;
} 

ソース2　※レイアウトの都合上一部改行している個所があります。

　関数宣言と前回実装した「setup()」関数に、以下の実装を加えます。

boolean setupGL(oes3d* pMe); 

boolean setup(oes3d* pMe){
        ISHELL_CreateInstance(pMe->a.m_pIShell, AEECLSID_GL, (void **)&pMe->m_pIGL);
        ISHELL_CreateInstance(pMe->a.m_pIShell, AEECLSID_EGL, (void **)&pMe->m_pIEGL);
        if(setupEGL(pMe) == FALSE)
                return FALSE;
        if(setupData(pMe) == FALSE)
                return FALSE;
        if(setupGL(pMe) == FALSE)
                return FALSE;
        return TRUE;
} 

　まず投影の設定ですが、ここでは視錐台、ビューポートの設定がポイントになります。「IGL_glMatrixMode()」でGL_PROJECTIONを指定して、投影の計算が行えるようにします。「IGL_glLoadIdentity()」は、内部的には行列計算の累積をクリアにするための処理ということになりますが、基本的に初期化と考えてもらって結構です。そして、「IGL_glFrustumx()」によって視錐台の設定を行います。OpenGL ESには「gluPerspective()」のようなGLUのヘルパー関数はありませんので、視野角などを自身で計算して設定を行う必要があります。指定する各座標は、投影面の大きさを中心からの座標で指定する必要があるので、視点である原点からの二等辺三角形の底辺を求める式「底辺＝2×高さ×tan(頂角の半分)」で求められます。ここでは、標準視野角である45°を想定し、ニアクリップの位置である高さを「10」としているので、「底辺＝2×10×tan(22.5)」となります。ここでは、中心からの長さが分かればよく、2を掛ける必要はないので近似値として「4.1」を使用します。

図11　視錐台とビューポートの設定

　また、取得した画面サイズを「IGL_glViewport()」によりビューポートに設定していますので、画面サイズに依存しないように投影面のx座標にアスペクト比を掛け合わせています。

※注3：ちなみに、OpenGL ESでは視点であるカメラ位置が原点(0,0,0)に置かれており、視線はz方向のマイナス、角度は(0,1,0)のやや上向きを向いています。

　次にライトの設定ですが、「IGL_glLightxv()」のパラメータでライトの位置と拡散光を設定しています。OpenGL ESでは、8つライトをサポートしていますが、ここでは1つしかライトを設定しないので「GL_LIGHT0」を指定しています。ライトの位置に関しては、x、y、z、wで指定しますがwが「0」の場合、無限遠となるのでx、y、zの位置から無限遠上にライトがあるということになります。ライトの種類については「GL_DIFFUSE」で特定方向から来る光である拡散光を指定して、オブジェクトの陰影が分かりやすいようにしています。そして、「IGL_glEnable()」で「GL_LIGHTING」「GL_LIGHT0」を有効にして、設定したライトを有効にしています。また、このときに「GL_NORMALIZE」による法線の正規化を行わないと、設定した法線が有効にならないため注意が必要です。以上の設定により、青い拡散光が立方体に対して照らされることになります。

　最後に、用意した立方体のデータを操作するための準備を行います。「IGL_glEnableClientState()」に「GL_VERTEX_ARRAY」と「GL_NORMAL_ARRAY」を指定して、それぞれのデータ配列を有効化し、「IGL_glMatrixMode()」で「GL_MODELVIEW」を指定して、3Dオブジェクトの表示に関する計算を設定します。この際、「GL_PROJECTION」と同様に「IGL_glLoadIdentity()」を実行しておきます。