明石海峡の強風にあおられても、大丈夫?:独学! 機械設計者のための自動制御入門(4)(2/4 ページ)
フィードバック制御をしているからといって、すべてを目標値にできるわけではない。例えば車が風にあおられたときは?
伝達関数の演算に慣れよう
まず、最初の解析テーマについて考えてみよう。車が横風を受けたときに、前ページ図1のブロック線図の入出力の関係はどうなるだろうか。草太、考えてみてくれへん?
前回の復習を兼ねて、皆さんも各自で考えてみてください。
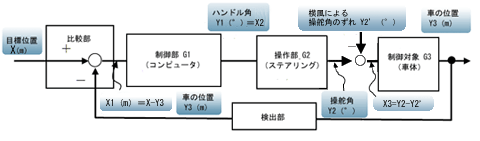
図1の制御部G1の入力は、車体をX1 (m)横に移動させろ、という指令で、その出力は操作部G2に対して、ハンドルをY1(°)回せという出力ですから
Y1/X1=G1 (1)
です。
操作部G2の入力はハンドルをX2(°)回転させろ、という指令で、それに対して出力は「車のタイヤをY2 (°)回せ」ということですから
Y2/X2=G2 (2)
です。
車のタイヤがX3 (°)回転すれば、車体は進行方向に対して横にY3(m)動きますから
Y3/X3=G3 (3)
ですが、車体の走行特性G3の入力X3は今回は、横風によって
X3=Y2−Y2’ (4)
となりますから、(3)から 、
Y3=G3・X3=G3・(Y2−Y2’) (5)
となり、(2)から(5)は、
Y3=G3・(Y2−Y2’)=G3・(G2・X2−Y2’) (6)
となります。
さらにG2の入力X2はそのままG1の出力Y1に等しいですから、(1)より
Y3=G3・(G2・Y1−Y2’)=G3・(G2・G1・X1−Y2’) (7)
となり、これを、整理すると、
Y3=G3・G2・G1・X1−G3・Y2’ (8)
となります。
G1の入力X1は、目標値Xと出力値Y3との偏差ですから、
X1=X−Y3 (9)
(8)と(9)から、Y3は結局、
となります。
開ループシステムの伝達関数Goは
Go=G1・G2・G3 (11)
だったから、(10)は、式(12)とも書けるね。
よく分かってるやん
開ループシステムの伝達関数Goのゲインが無限大と見なしていいほど大きければ、
Go/(1+Go)⇒1
だから、(12)右辺第1項はXとなって、車の位置であるY3は、目標位置Xに等しくなるし、
G3/(1+Go)⇒0
ならば、(12)右辺第2項は0となって、横風による影響もなくなるってことか。逆にGoのゲインが小さいと、目標位置Xからずれてしまうんだね
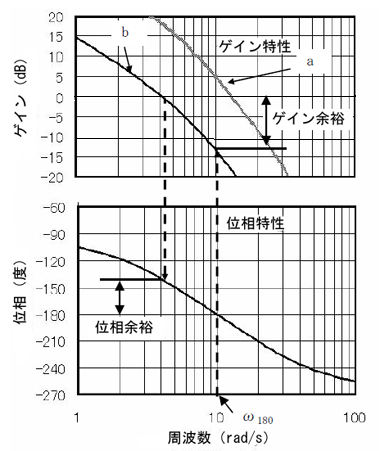
そういうことやね。実際、前回示した周波数応答曲線(第3回の図8)は、低周波域のゲインは無限大となるような特性だった
でも、周波数が高い領域ではゲインは無限大ではない。ということは、その領域では追従できないということか
そうや。これは、ある速度で目標値が変化するときの追従特性の話だから、いわゆる動特性の問題や。動特性についてはまた次の機会に説明するとして、式(12)に関して、注意しておかなければならないことがある
何?
さっき草太は、開ループ伝達関数Goの低周波ゲインが無限大であれば横風の影響を受けないようなことをいっていたけど、G3の低周波ゲインが無限大の場合には、必ずしもそうとはいえなくなるぜ
それは、そうだね。すると、横風によって車が目標位置とどのくらいずれるかを知るためには、ω⇒0のときのG3/(1+Go)のゲインの値を正しく知る必要が出てくるね。前回、伝達関数の各周波数応答特性は、入出力波形を実測することで求めることができるって教えてくれたけど、G3/(1+Go)の周波数応答特性はどうやって求めたらいいんだろう? G1、G2、G3はそれぞれ制御部、操作部、車という物理的な実態が存在するから実測方法をイメージできるけど、G3/(1+Go)の場合、入力と出力は何で、物理的な実態としては何をイメージすればいいの?
それはだな……
Copyright © ITmedia, Inc. All Rights Reserved.