猫とピンポン球と周波数応答特性:独学! 機械設計者のための自動制御入門(2)(3/3 ページ)
今回は、周波数応答特性について。猫が目の前を飛び交うピンポン球をキョロキョロ追いかける様子になぞらえて説明する
ボード線図
これで、『反応の遅れ』と『変化に対する過剰反応』を定量的に表現することができることが分かったやろ。ただし対象とする周波数は0 Hzから∞ Hzまであるから、すべての周波数を横軸に載せると、横軸がものすごく長くなる。そこで、周波数の対数を取ることにしている
対数表示にすれば広範囲の周波数を狭い直線領域に押し込めて表現できるからね
さらに入出力の振幅比をそのまま縦軸にするのではなく、振幅比の対数の20倍を取ることにしている。これを『ゲイン』と呼ぶのは知っているよな?
日本語に訳すと『利得』。最初聞いたときは、なんかしかつめらしい言葉だな、と思ったよ
まぁ、普通は『ゲイン』と呼ぶな。電気の増幅器の設計では増幅率とも呼んだりするけど、ここでは『ゲイン』と呼ぶことにしよう。それから、位相遅れの周波数特性と併記したものを『ボード線図』と呼んでいるのは知っているやろ?
知ってるけど、振動工学では『共振曲線』と呼ぶのに、制御工学では『ボード線図』と呼ぶのを聞いて、これもどうして同じ表現にしないのか不思議に思ったよ
『共振曲線』は、その名の通り固有振動との共振性を表現するのが目的だから、横軸は普通、固有振動数との比とするな。縦軸は振幅比だ。もっとも、固有振動数が不明な場合は横軸に振動数そのものを取る。一方『ボード線図』の場合は横軸は周波数(振動数)そのもので、何かとの比を取ることはない。そして縦軸は『振幅比の対数』を取る。振幅比の対数というところが共振曲線との大きな違いであり、かつ制御系設計でボード線図が利用される最大の理由でもある
最大の理由って、何?
いまここでそれを説明するより、具体的事例が出て来たときに詳しく説明した方がお前の頭に入りやすいやろ。だからそれはあとで説明することにするわ。それから、共振曲線では、普通はそれほど位相特性を重視しない。共振振幅がどのくらいになるのかを知るのが共振曲線を作成する主な理由だからだ。しかしボード線図では、どちらかといえば、位相特性の方が知りたい情報なんだ。これも共振曲線との大きな違いだ
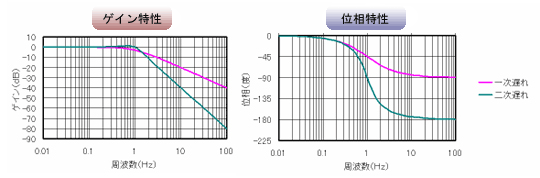
じゃあ、具体的なボード線図の例を紹介しておこうか。図7のピンクの線は、代表的なボード線図で『一次遅れ』のボード線図だ
だんだん出てきたね、数学的表現が。次は二次遅れでしょ?
まず、なぜ『一次遅れ』って呼ぶと思う?
位相が直線的に遅れるから?
違うな。特性を数学的に表現すると一次の微分方程式となるからだ。じゃあ、なぜわざわざ『遅れ』という言葉を付けるのかな?
分かりましぇ〜ん
私は専門家ではないから、この説明が正しいかどうか分からんけど、次のように考えている。制御、特に安定性においてもっとも重要な特性は『遅れ』だ。だから、この『遅れ』を強調するためにわざわざ『遅れ』という言葉を付けていると私は理解しているんだ。一次遅れ特性であれば、位相遅れは0からスタートして90度までしか遅れない。しかし図7のグリーンで示した二次遅れ特性だと、180度まで遅れる。つまり、次数が1つ増えるごとに位相遅れが90度ずつ増えていくんやな
位相の遅れの様子が、方程式の次数で異なっているといいたいわけだ。逆にいうと、方程式の次数が分かれば遅れの様子も分かり、遅れの様子が分かれば、システムを微分方程式で表現したときの次数が分かるってことだね
実際はそんなにすっきりしていなくて、遅れ特性にはそのほかに『無駄時間遅れ』というのがある
そういえばそんなんあったな。ゲインは変化しないけど、位相だけ無駄に遅れるってやつ。情報が伝わるまでの遅れを『タイムラグ』って呼ぶけど、このタイムラグが『無駄時間遅れ』っていうのを覚えているよ。これは『情報の遅れ』だね
それそれ。システムの中にこれが入っていると、さっき説明した、次数に応じて90度ずつ遅れが増えるという法則が成立しなくなるんだ。しかし無駄時間遅れのない素直なシステムでは、さっき説明したように、次数が増えると遅れが90度ずつ増えるってことを覚えておいて損はない
は〜い
ところで、ボード線図は具体的にどうやって作ると思う?
そうだね。計測するのかな?
実機の特性についてはそのとおりだ。サーボアナライザという便利な計測器があって、これを使うんや
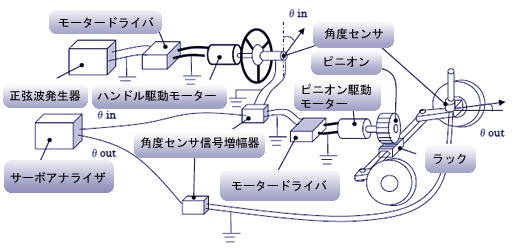
例えば、図8のようなステアリングシステムの周波数応答特性を計測することを考えてみましょう。ハンドル操作は本来人間が行いますが、人間の力では周波数に対応したハンドル操作を正確にはできません。そこで強力なモータで動かすことにします。正弦波発生器から正弦波信号を受けて、モータがハンドルを左右に回転させます。
筆者注
1.図8はあくまで説明用の仮想実験装置です。このようなシステムが実在するかどうかは分かりません。
2.通常はサーボアナライザの内部には正弦波を生成する装置が内蔵されていますから、別に正弦波発生器を用意する必要はないでしょう。
ここで、周波数応答特性の基準となる入力を正弦波発生器からの信号ではなく、ハンドルの回転角θinとします。正弦波発生器から出た信号を入力とすると、ハンドルを駆動するモータの特性も入ってしまうからです。計測したいのは、ハンドルの回転角θinに対しての操舵角θoutの周波数応答なのです。
図を見れば細かい説明は不要だと思います。ハンドル回転角θinとタイヤの操舵角θoutをセンサでそれぞれ電気信号に変換し、さらに増幅してサーボアナライザの出力信号ポートに入れると、サーボアナライザは、周波数を自動的に変えながら、入出力信号のゲイン、位相遅れを計算し、その結果をボード線図にしてディスプレイ表示したりプリントアウトしてくれます。
実測するとなると、『物』が必要になるじゃん。設計するときには『物』がないけど、どうするん?
そのときは、システムを運動方程式や状態方程式で表現する必要が出てくるな
やっぱり数式が出てくる
別に心配せんでもええで。実際のシステム構成には購入品も多いから、その特性についてはメーカに頼めばメーカの方で計測してくれるし。あとでシステムの特性改善について話をすることになると思うけど、基本的手法は確立しているから、慣れてしまえば、運動方程式を立てて、ややこしい制御理論を駆使しながら設計する方法を知らなくても、制御系の設計ができるようになるよ
とにかく、フィードバックシステムが不安定となる原因は、システムの構成要素に内包する『情報や応答の遅れ』と『変化に対する過剰反応』だってことは理解してくれたかな
感覚的には、よく分かったけど……
そして、それらの特性を定量的に表現したのが『周波数応答特性』だ。特に覚えておいて欲しいのは、周波数応答特性には、構成要素に対して入力と出力間のゲイン(振幅比)と位相遅れの2つの特性があるってことだ。2つあるってことが重要なんだ
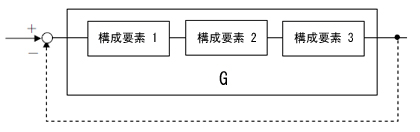
図9のような、制御システムの中のすべての構成要素を繋いだ全体システムG(フィードバックを構成する前のシステムを開ループシステムと呼ぶことがあります)の出力を入力側にフィードバックして、目標値に追従するようなフィードバックシステム(フィードバックを構成したシステムを閉ループシステムと呼ぶことがあります)を構築したとき、Gのゲイン特性と位相遅れ特性によって、そのフィードバックシステムが安定か不安定かが決まってきます。
草太は、開ループシステムGの「情報や応答の遅れ」と「変化に対する過剰反応」が、ループを閉じたときのフィードバックシステムを不安定とする原因である、という定性的な説明に、感覚的には理解できたようですがもう1つ納得していないようです。どうやら、不安定が発生したりしなかったりする理屈やその発生限界について、もう少し細かいことを知りたいようです。
◇
次回はフィードバックシステムの不安定発生メカニズムおよび発生限界について、ボード線図を使って定量的に説明します。
*** 一部省略されたコンテンツがあります。PC版でご覧ください。 ***
Copyright © ITmedia, Inc. All Rights Reserved.