直交配列実験を基にした重回帰分析の実務：Excelで学ぶ実験計画法の基礎（4）（3/5 ページ）

品質管理のための代表的な統計手法である実験計画法について、実践的な手法を短期間に習得したいと希望している読者に向けて、Excelを使って効率的に独学できるような解説を行う。

[菅民郎・福島隆司／株式会社エスミ，＠IT MONOist]

重回帰分析とは

　重回帰分析とは、特性値を複数の因子で予測するための方法です。分析を実行した際に初めに検証するのは予測の精度です。予測の精度を示す統計量は補正R2と呼ばれる値で、0から1までの範囲の値を取り、予測の精度が高いほど高い値になります。最低の目安は0.25で、理想は0.5以上です。0.25未満の場合は、誤差が大きい結果なので、それ以降の結果の考察は控えた方がよいでしょう。分析の結果の補正R2は0.996で1に近く、非常に予測の精度は高いといえます。補正R2はデータに対する値です。

　母集団についても結果に意味があるのか、分散分析にて有意性検定を実施した結果が分散分析表です。有意Fの下に表示された値がP値で、判定のルールはこれまでと同様0.05以下であれば、母集団においても予測ができると判定します。分析の結果の有意Fは0.000で重回帰分析の結果は有意であるといえます。

　重回帰分析は、次に示す重回帰式と呼ばれる線型1次式で特性値を予測します。

　yは特性値、x_pは因子で因子の数だけ項が存在します。a_pは式の係数、a₀は定数項です。yとx_pはデータが存在するので、重回帰分析は、予測値と実際の値の誤差が最も小さくなるよう式の係数a_pと定数項a₀を計算します。係数と定数項の値は係数の下に一覧で表示されます。分析の結果の重回帰式は、

となります。x₁は作業員、x₂は設備、x₃は手順です。各因子の水準の効果は、この係数の値を使って検証します。ちなみにx_pの取る値は0か1です。作業員の場合、1が「5年以上」、0が「5年未満」に対応します。そうすると、すなわち「5年以上」の場合、a_pa_pの値は−39.750×1＝−39.750で、すなわち「5年未満」の場合、−39.750×0＝0となります。

　この値の差の大きさ39.750は、「5年以上」と「5年未満」の不良品の個数の予測値の差で、因子：作業員の水準の効果を表します。すなわち、係数a_pが因子の効果を示す値になるのです。ほかの因子も同様に解釈すると、設備の効果は3.750で、手順の効果は17.250になります。これらの値から、因子の影響度の大きさの比較ができます。

　分析の結果では、作業員の効果が最も大きく、次に手順、設備と続きます。作業員のキャリアが不良品の個数に最も影響しているということです。作業員の定着による作業習熟度を高めることが、不良品の個数の低減に最も効果的であるといえます。一方、設備の効果は小さく、ほとんど不良品の個数に影響していません。不良品の個数の低減のため、設備を変更するのは、意味のない対策であるといえます。

　ほかに重回帰分析の本来の目的である予測のテクニックを利用することで、今回の事例のような場合、ある条件における不良品の個数がシミュレーションできます。方法は簡単です。シミュレーションしたい条件を決め、その条件に該当する01データを重回帰式に代入して予測値を計算します。例えば、作業員が「5年以上」で、設備が「A」、手順が「B」の工程の不良品の個数をシミュレーションしたい場合、重回帰式のx₁に1、x₂に1、x₃に0を代入した値を計算します。すると、

y＝−39.750×1−3.750×1＋17.250×0＋63.500＝20.000

となります。この20が予測値で、シミュレーション値です。作業員が「5年以上」で、設備が「A」、手順が「B」の工程の不良品の個数は平均20個であるといえます。数値に関する留意点は、重回帰分析の予測値は平均値で、ズバリの値ではないということです。当然誤差を含むわけですが、その誤差の目安になるのが、回帰統計に表示された標準誤差で、分析の結果では1.458です。不良品の個数はだいたい20±1.458になると表現できます。このテクニックを利用することで、架空の工程に関する不良品の個数の推測が可能になります。

　以上が、予測の方法を利用したシミュレーションのテクニックでしたが、因子の効果の分析と併せて有効な方法です。ぜひチャレンジしてみてください。

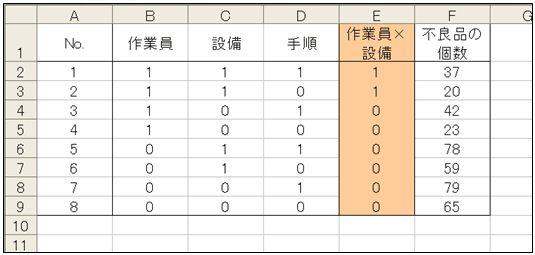
　特に述べませんでしたが、これまでの分析は、因子間に交互作用がないことを前提にした分析です。そのため、交互作用の大きさに関する情報は得られません。仮に、作業員のキャリアが不良品の個数に影響するとして、設備が「A」の場合は「B」より、先に計算した39.750より、さらに不良品の個数が低減すると考えられる場合、交互作用が存在することになります。交互作用の効果の大きさを検証したい場合は、対象となる因子の01データを掛けた交互作用の列を準備して重回帰分析を実行します。作業員と設備の交互作用の大きさを分析したい場合は、図14のようなデータセットを準備します。

図14　作業員と設備の交互作用を分析

　解釈などの詳細は割愛します。ただし、すべての場合で交互作用の効果が分析できるわけではないことを覚えておいてください。できるか否かは、実験に取り上げる因子の数や、直交表への割り付け方に依存します。