台車を狙いどおりに転倒させるよう計算しよう:ピタゴラスイッチの計算書を作ろう(4)(2/4 ページ)
台車が直線スロープを降り、ストッパと衝突したときにきちんと転んでほしい。 さあ錘(おもり)の重量はどれくらいにしよう?
ロック機構の設計評価
草太は以下のようにロック機構を設計しました。
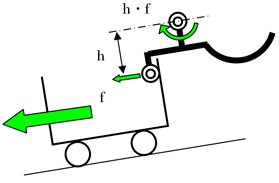
草太「台車をロックしていないときは安定する。でも、台車をロックするとやじろべえの支点が台車から作用する力の作用線上より上にあるので、台車が引っ張られて、やじろべえは右に回転してロックが外れてしまう。反対に、支点が台車から作用する力の作用線上より下にあると左回転するから今度はロックが外れにくくなる」
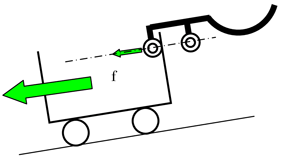
草太「だから図4.2(b)のように、やじろべえの支点は台車から作用する力の作用線上にしておく。そうすれば、台車の質量の大きさに関係なくロックは外れないよ」
銀二「つまり、台車から作用する力の作用線上にロック機構の支点があれば台車がどんなに重くても台車は繋留できるってわけだ」
草太「でも、ロック機構自体がアンバランスで、例えば支点を回転中心とした右回転のモーメントが大きければ、台車が軽い場合にはゲートからボールが来る前に台車はロックから外れてしまう。反対に左回転にモーメントが大き過ぎると、ボールが網の中に入ってもロックが外れない可能性だってある。だから、ロック機構もそれ自身でほぼバランスさせる必要がある。そうすれば、必ずロックは外れると思うんだ」
銀二「なるほど。なかなか説得力のある説明だね。さすが私の甥(おい)っ子だ」
草太「写真4.1を見てもらえば分かると思うけど、だいたいバランスしているでしょ?」
銀二「そうだね。うまくバランスしているね。別に計算式を使わなくたって設計はできるし、実際の設計の多くはいまのような定性的な考え方に基づいて図面を描いているんだ。でもお前がしてくれた説明がなければ、ロック機構の図面を見ただけでは、どうしてこのような構造にしたのかまでは分からない」
草太「設計計算書というと、計算式ばかりだと思っていたけど、図4.2のような説明図も立派な設計計算書となるんだね」
銀二「そういうことだよ」
銀二叔父さんは、草太の用意した説明図を満足げにながめています。ロック機構の設計については申し分ないようです。次に草太は、台車の設計について説明をしてきます。
草太「台車はね、子供用の弁当のおかず入れを利用して作ってみたよ。写真2を見てもらえば特に説明は要らないと思うよ。問題は、直線スロープ2を降って、ストッパと衝突したときに、台車が回転してくれるかどうかだね。実は、叔父さんが来る前にやってみたんだけど、このままでは台車はうまく転倒しないんだ。そこで台車に錘(おもり)を付ける必要があるんだけど、ここからが、台車の本当の設計だと思うんだ」
銀二「そうだな。台車の機能は、直線スロープ2のストッパに衝突して、台車が回転し、中のボールを落とすことにある。衝突した台車が回転するために必要な条件はなんだと思う?」
草太「う〜ん、難しいな。だけど、ここでもエネルギーの考えを使えばなんかそれらしい計算ができそうだね」
銀二「草太、まんがれ!」
草太「何それ? “ま”んがれって……」
台車に使われていた小さなおかず入れ。これを見ていた銀二叔父さんは、兄夫婦、つまり草太の両親から見せられたホームビデオを思い出していました。
銀二「幼稚園の運動会で、草太が徒競走をしていたんだが、そのころ2歳だったお前の妹が、『そーたくん、まんがれ!』って応援していたんだよな。『頑張れ』を『まんがれ』、スパゲティを『スパゲッキィ』、ポケットを『ポペット』っていっていたリョコピョンも、もう大学2年生なんだなあ……」
草太「そうだったっけ? そんなの覚えてない」
草太は、頭をかきながら目をそらしました。“叔父さんってば、いつまでたっても僕や涼子を子供扱いだ”と、くすぐったいような、くやしいような思いがしました。まあ、この卒業課題の成果で叔父をうならせるしかあるまい――草太は気を取り直します。
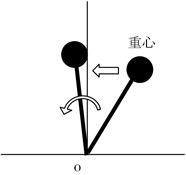
草太「思い出話は、後で酒でも飲みながら。さあさあ……まず転倒するっていうことを技術的に翻訳すれば、衝突点を支点として回転運動をしたときに、重心が支点を通過する鉛直線を越えるってことだよね(図4.3)」
銀二「あ、ああ。そうだよ」
台車の設計についての説明は、まだ続きます。
編集部より、読者の皆さまへ
以降で出てくる数式をメモ帳やノートなどに書き取るなどして、実際に計算しながら読み進めてみてください。より理解が深まります。
またまたエネルギーの保存が登場だ
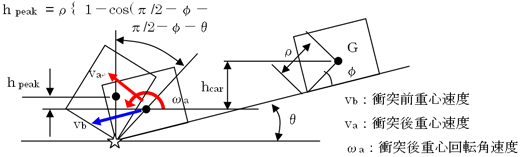
草太「つまり台車がストッパと衝突して回転したときに、台車の重心位置が垂直になるまで揚がって、そのときに台車が回転速度を持っていればそのまま倒れるはずだ。衝突直前の台車の速度vb はエネルギーの保存式から簡単に計算できる。上の図4.4から、以下の式のようになるね」
草太「Mcarが台車の質量を意味しているってことは説明不要だね。hcarはロックが外れて台車がストッパに衝突するでの移動段差だ。同様に、衝突以降の運動についてもエネルギーの保存を考えると次の式が成立する」
草太「ここで添え字a は衝突直後(after)を意味しているよ。h は衝突直前を基準としたときの台車の重心高さで、Jcarは重心周りの台車の慣性モーメント。衝突点を回転中心とすると回転半径ρに対して、こう」
草太「だから(4-2)は次のようになる」
草太「台車が回転して倒れるためには、台車が真上に倒立したときに、回転角速度ω が0より大きくなければならないから、以下の式が成り立つはずだ」
草太「つまり衝突直後の台車の回転角速度ωa が分かれば転倒するかどうか分かる」
銀二「まんがれ! まんがれ! そ・う・たっ!」
草太「もーっ! まんがれまんがれいわないっ。 ……で、ωa は、どうやって求めるかというと、前回出てきた反発係数eを使って計算できる。つまりストッパは、衝突前後で速度は0だから……」
草太「添え字のb は衝突前のbeforeを意味している」
草太「だから、(4-5)は以下のようになる」
草太「hpeakは台車の重心位置を計算すれば簡単に求められるし、ストッパに衝突する直前の台車の重心速度vb は(4-1)で計算できる。よって上の式を満足するように台車の質量Mcarや重心位置ρを決めてやればいいんじゃないの?」
銀二「惜しいね。ちょっと違うな」
草太「もしかして、反発係数のところ?」
銀二「そうだよ」
Copyright © ITmedia, Inc. All Rights Reserved.