スクラムのミニチュアモデル:「失敗学」から生まれた成功シナリオ(1)(1/2 ページ)
長年にわたりおびただしい数の失敗事例を研究してきたことで見えた! 設計成功の秘訣(成功シナリオ)を伝授する。(編集部)
筆者は失敗学と称して、いくつかの一般的・共通的・抽象的・反復的なシナリオを使って、多くの失敗事例をグループ分けしてきた。今回取り上げる「スクラム(*1)のミニチュアモデル」もそのシナリオのようなものである。このコラムでは、失敗よりも成功する設計に注目して、役に立ちそうなシナリオを紹介していく。
ガラスの張り合わせ実験がうまくいかない
昨年、研究室の学生が、2枚のガラス板を張り合わす実験に苦しんでいた。彼は、2枚のガラス板の間にガラスの粒子を含むペーストをサンドイッチした。次にペーストを塗ったところだけを、ガラス板の上面からレーザを照射して、局所加熱によって溶融・接合させたかった。
ところが、何度やってもガラス板が割れてしまうのである。長方形のガラス板の四辺にレーザで一筆書きして接合させたいが、一辺を書いたところで始点と終点の両端で割れるのである。
有限要素法(*2)で計算すると、ガラス板の両端で破壊強度を超える応力が発生していたから、学生は仕方がないという。しかし、どこから壊れるのか、どうして壊れるのか、どうやって防ぐのかと筆者が聞いても、学生は割れたガラス板と計算結果を見せるだけである。
筆者は、こういうとき、何かアナロジー(類推)を使って説明できないか、と必死に考えることにしている。そうしないと、すべてがケースバイケースに見えて、個々の条件ごとに計算または実験をしないと結果が読めない。それでは困る。
押競饅頭(おしくらまんじゅう)のミニチュア
そこで筆者は、ガラス板を「押競饅頭」している人たちのミニチュアモデルに見立てた。
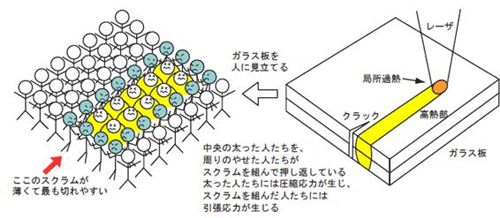
図1に示すように、レーザを当てた部分だけが熱膨張して、人々はお相撲さんの着ぐるみをまとったように、熱くて「太った人たち」になる。しかし、その周りにはレーザの熱が伝わってこないから、そこの周りの人たちは変わらず、冷えて「やせた人たち」のままである。でも熱くて太った人たちが押競饅頭のあんのように押してくるから、周りの冷えてやせた人たちは互いにスクラムを組んで必死に耐えることになる。
つまり、熱くて太った人たちはもっと広がりたいのにギューギュー詰めになり、そこには圧縮応力(*3)が働く。一方で、冷えてやせた人たちはスクラムした腕が切れるように引っ張られるが、そこには引張応力(*4)が働く。最後にはスクラムのどこか1カ所で腕がほどけて全体が崩れてしまう。クラックが伸展して割れてしまう。最も割れそうなところは自由表面に近いガラス板の両端である。図を見てもそこのスクラムの層は薄く切れやすそうである。
やせた人たちのスクラム
そうと分かれば後は簡単である。「やせた人たちのスクラム」を作らなければよい。
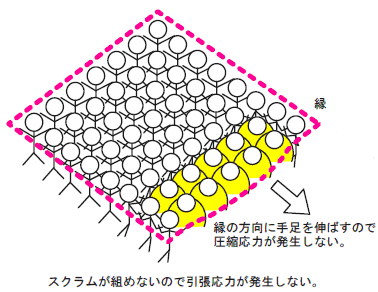
例えば、ガラス板のギリギリの「縁(へり)」をレーザで加熱する。これは図1の1列目と2列目の人たちがいなくなることを意味する。
図2(a)に示すようにやせた人たちはスクラムを1周回せなくなり、太った人たちは手足を伸ばして縁の方に寄れる。スクラムを組めないということは引張応力がなくなったことを意味し、太った人が手足を伸ばせるということは圧縮応力もなくなったことを意味する。
編集部注
*1 スクラム:ラグビーのゲーム内で、ゲーム再開の際に選手同士が身体を組み合いボールを取り合うこと。ここでは「複数の人が身体を組み合っている状態」を指している。
*2 有限要素法:数値解析手法。複雑な形状を細かく分割し、方程式で単純化していくことで、形状の持つ、ある1つの傾向の解を導く。構造力学の分野でよく使われる。
*3 圧縮応力:材料の、ある面積当たりに掛かる圧縮によって生じる内力。
*4 引張応力:材料の、ある面積当たりに掛かる引張によって生じる内力。
Copyright © ITmedia, Inc. All Rights Reserved.